© 1998 - 2022 Wolfgang Neundorf
Stand: 20.08.2022

Gerade mit dem Zeitbegriff sind viele Missverständnisse und Fehlinterpretationen verbunden. Auf einige dieser Zusammenhänge im physikalischen Sprachgebrauch gehen die folgenden Ausführungen ein.

Die Zeit ist 1) kein empirischer Begriff, der irgendvon einer Erfahrung abgezogen worden. Denn das Zugleichsein oder Aufeinanderfolgen würde selbst nicht in die Wahrnehmung kommen, wenn die Vorstellung der Zeit nicht a priori zum Grunde läge. Nur unter deren Voraussetzung kann man sich vorstellen: dass einiges zu einer und derselben Zeit (zugleich) oder in verschiedenen Zeiten (nach einander) sei.
2) Die Zeit ist eine notwendige Vorstellung, die allen Anschauungen zum Grunde liegt. Man kann in Ansehung der Erscheinungen überhaupt die Zeit selbsten nicht aufheben, ob man zwar ganz wohl die Erscheinungen aus der Zeit wegnehmen kann. Die Zeit ist also a priori gegeben. In ihr allein ist alle Wirklichkeit der Erscheinungen möglich. Diese können insgesamt wegfallen, aber sie selbst (als die allgemeine Bedingung ihrer Möglichkeit) kann nicht aufgehoben werden.
Immanuel Kant (1724 - 1804)

Wieso weiß die Uhr, wie spät es ist?

Vorbemerkungen

Die Kantsche Zeitauffassung hier zu diskutieren, soll mein augenblickliches Anliegen nicht sein. Aber diese ist mir immer noch sympatischer als jene Standpunkte, die der Zeit eine selbständige reale und objektive Existenz zusprechen (vgl. Pygmalion-Effekt - Zeit).

Es sind eben zwei Aspekte des “Zeitproblemes” zu beachten: Zum einen haben wir es mit dem Zeit-Begriff zu tun und zum anderen spielt die Zeit als messbare physikalische Größe eine nicht gerade unbedeutende Rolle. In Pygmalion-Effekt - Zeit bin ich auf wichtige Seiten der Begriffsbildung eingegangen, wobei es um das Problem ging, dass gemeinhin - und dies gilt für die Physik als Wissenschaft in gleichem Umfang - die Begriffe als lineare Abbilder realer Gegebenheiten betrachtet werden. Also:

Es gibt den Zeit-Begriff - also muss es auch das Objekt Zeit geben.

Die zweite nicht weniger wichtige Seite dieser Medaille befasst sich mit der Zeit-Messung. Dies nun einmal setzt eine physikalische Größe voraus, die wir Zeit nennen und für die es exakte Vorschriften der Messung gibt. Dies geht so weit, dass mit Hilfe bestimmter technischer Einrichtungen es möglich ist, einen Zeitmaßstab zu definieren. In Deutschland beispielsweise übernimmt die Physikalisch-Technische Bundesanstalt (PTB) die Rolle der Realisierung eben jenes Zeitmaßstabes in Gestalt der SI-Basiseinheit Sekunde.

Wenn es also Prozesse gibt, die einen weitgehend stabilen, eindeutig reproduzierbaren und von allen möglichen Umwelteinflüssen unabhängigen Zeitmaßstab bereitstellen, so sind wir - dies könnte der Eindruck sein - der Objektivierung der Zeit ein beträchtliches Stück näher gekommen:

Die Prozesse in den Atomuhren des PTB verkörpern die objektive Zeit.

Also sind meine Gedanken, den Zeitbegriff betreffend, doch nicht richtig - könnte man meinen. Aber: Uhren sind physikalische Systeme, die - wie auch immer die technische Umsetzung konkret ausfallen möge - einen streng periodischen Prozess realisieren. Einen solchen Prozess finden wir beispielsweise in der Erdrotation, die uns den Zeitmaßstab Tag bereitstellt. Dieses Intervall lässt sich weiter untergliedern in die Einheiten Stunde, Minute und Sekunde. Hier eine Textpassage der Web-Site des PTB ( Geschichte der Zeiteinheit):

Das für den Menschen natürliche Zeitmaß ist der durch die Erdrotation definierte Tag. Der wahre Sonnentag (von einem Sonnenhöchststand bis zum nächstfolgenden am gleichen Ort) hat wegen der Schiefe der Ekliptik und der Ellipsenform der Erdbahn eine recht ungleichmäßige Dauer. Dem Drehwinkel der Erde proportional und daher eher gleichförmig ist die mittlere Sonnenzeit an einem Ort, deren Zeitmaß der mittlere Sonnentag dm ist. Mit Hilfe von Uhren wird dm weiter aufgeteilt in 24 Stunden zu je 60 Minuten zu je 60 Sekunden. Die Festlegung der Dauer der Sekunde als dem 86.400. Teil des mittleren Sonnentages war im Grunde willkürlich, ein Teil unserer tradierten Kultur. Eine formale Definition dieser Sekunde als verbindliches Zeitmaß im Sinne des Internationalen Einheitensystems SI hat es nie gegeben. Die auf den Nullmeridian bezogene mittlere Sonnenzeit wird Weltzeit UT (Universal Time) genannt, die ursprüngliche und heute noch populäre Bezeichnung war GMT (Greenwich Mean Time).

Dies ist die offizielle Definition der SI-Sekunde:

Die Sekunde ist das 9 192 631 770fache der Periodendauer der dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids ¹³³Cs entsprechenden Strahlung.

Hier noch einmal ein Satz aus dem ersten Zitat:

Mit Hilfe von Uhren wird dm weiter aufgeteilt in 24 Stunden zu je 60 Minuten zu je 60 Sekunden. Die Festlegung der Dauer der Sekunde als dem 86.400. Teil des mittleren Sonnentages war im Grunde willkürlich, ein Teil unserer tradierten Kultur.

Um dies aber zu können, ist es zweckmäßig, sich anderer zyklischer Prozesse zu bedienen. Und die einfachste Uhr, die mit mechanischen Mitteln realisiert werden kann, ist das Pendel. Nun sollte die Schwingungsdauer eines Pendels weitgehen unabhängig sein von lokalen Umwelteinflüssen: hier seien beispielsweise Temperatur und Luftdruck genannt. Dass diese Forderung in praxi immer nur näherungsweise erfüllt werden kann, ist allgemein bekannt. Und bekannt auch ist, dass eine Uhr um so “besser” ist, je weniger ihr Lauf von eben jenen lokalen Einflüssen abhängt. Dies erfüllen die sog. Atomuhren mit hoher Präzision. Warum das so ist, soll im Folgenden nicht erörtert werden. Hier geht es darum, dass Quantenprozesse eben nicht oder nicht nachweisbar von außen beeinflussbar sind. Dies ist ein Kapitel für sich. Die Energieniveaus in den Atomen und die damit korrespondierenden elektromagnetischen Frequenzen sind eben absolut stabil und von außen nicht zu verändern.

Die relevanten Parameter einer Uhr müssen also äußerst stabil sein. Und der mit Hilfe einer Uhr realisierte Zeitmaßstab darf nur abhängen von einem Parameter:

Und dieser Parameter ist die allseits beliebte und bekannte Zeit!

Damit wären wir beim Thema angekommen: Wieso weiß die Uhr, wie spät es ist.

Uhren

Beeindruckend ist sie durchaus - die Computertechnik. Was unsereins heutzutage sich auf den Tisch an leistungsfähiger Technik stellen kann ist schon überwältigend. Und das alles zu zivilen Preisen! Wer hätte das vor Jahren auch nur geahnt. Die technische Entwicklung hat die blühendste Phantasie überflügelt. Die „Kästen“ werden immer kleiner und Leistung wächst - anscheinend - in’s Unermessliche. Annähernd jedenfalls. Da stecken in einem Computer Millionen und Abermillionen von Schaltelementen, die vor zwanzig Jahren ganze Säle ausgefüllt hätten. Von den Kosten ganz zu schweigen. Das alles passt auf einen ordinären Schreibtisch. Und schnell sind sie, diese Wunderwerke der Mikroelektronik! - Wie schnell, das gehört zu den wesentlichen Leistungsmerkmalen eines solchen Gerätes. Ein wichtiges Charakteristikum für diese Geschwindigkeit ist die Taktfrequenz. Wird diese Frequenz mit 100 MHz angegeben, kann man getrost davon ausgehen, eine „lahme Krücke“ vor sich zu haben. Doch stelle man sich vor, die Angabe „100 MHz“ heißt, der Mikroprozessor führt intern pro Sekunde 100 Millionen „Elementaroperationen“ durch. Der Prozessor muss funktionieren und in ihm alle Funktionseinheiten. Kein Bit darf verlorengehen. Diese zeitliche Koordinierung wird von einem Taktgenerator vorgenommen, so dass sämtliche Prozesse wirklich synchron ablaufen und kein - auch nicht ein - Schaltelement aus der zeitlichen Reihe tanzt. In einem Mikroprozessor laufen viele parallele Prozesse ab. Der alles koordinierende „Masterprozess“ geht aus von einem geradezu unanständig primitiven quarzgesteuerten Oszillator. Gedankenverloren gehe ich die Straße entlang. Irgend jemand spricht mich an. Ob ich nicht sagen könne, wie spät es ist. Ich kann. Ich schaue auf die Uhr und gebe die gewünschte Auskunft. Dann gehe ich weiter. Eine Frage dabei kommt mir in den Sinn. Will ich die Uhrzeit wissen, so habe ich eine Uhr, welche mir diese Information bereitstellt. Nur: wieso eigentlich - verdammt noch mal - „weiß“ die Uhr überhaupt, wie spät es ist?

Was haben beide eben behandelten Angelegenheiten gemeinsam? - Da sei einmal der Quarzgenerator genannt. Im Falle einer Quarzuhr besteht diese Gemeinsamkeit in jener elektronischen Schaltung, deren Bestandteil ein Quarzkristall ist, der mit Hilfe dieser Schaltung in ungedämpfte Schwingungen versetzt wird. Dies ist die Gemeinsamkeit. - Wir aber wollen außerdem herausfinden, was beide Dinge nicht gemeinsam haben. Nichtgemeinsamkeiten gibt es in Hülle und Fülle. Einer dieser signifikanten Unterschiede aber wird uns der Antwort auf die Zeitfrage ein gutes Stück näher bringen. Herauszufinden, was damit gemeint ist, soll unsere nächste Aufgabe sein. Um diese Nichtgemeinsamkeit aufzuspüren, muss ich etwas weiter ausholen. Als erstes formuliere ich ein „Wechselwirkungsprinzip“, welches - auch für die weiterführenden Überlegungen - eine Schlüsselrolle übernehmen wird:

Alles hängt irgendwie mit Allem zusammen und verändert sich in gegenseitiger Abhängigkeit. Es gibt kein System, welches nicht mit weiteren Systemen im Zusammenhang steht, aber nicht jedes System steht (gleichzeitig) in Verbindung zu jedem anderen System.

Abbildung 1

Dies ist eine recht allgemeine Begriffsbestimmung, die aber - und das ist sehr wichtig - uns mit Sicherheit ein rechtes Abbild der Realität bietet, nicht eingeschränkt durch gar zu spezielle Vorstellungen, Hypothesen und Theorien. Diese Allgemeingültigkeit wird erkauft mit der Nichtbeantwortbarkeit konkreter Fragen. Aber - und hier halte ich es wie die etablierte Physik in manch anderer Beziehung - alles einem solchen Prinzip Widersprechende können wir getrost ausschließen. Diese Grundhaltung könnte zum Schiedsrichter werden bei der Entscheidung, ob etwas möglich ist oder auch nicht. Trotzdem müssen wir konkreter werden. Konkret genug, um überhaupt voranzukommen. Ausreichend allgemein muss es bleiben, um nicht in ausgetretene Pfade abzurutschen.

Fangen wir an bei den Begriffen. Was ist ein System? - Das weiß natürlich ein jeder. Dennoch wollen wir uns auf bestimmte Gesichtspunkte dieser Angelegenheit konzentrieren. Hierzu dient als einfaches Beispiel ein einfaches mechanisches Systems mit einfachen Gesetzen. Die in Abbildung 1 skizzierte Anordnung ist Bestandteil traditioneller Pendel-Uhren. Das „zeitbestimmende Element“ solcher Uhren ist ein Teilsystem mit der Bezeichnung „Pendel“. Der Einfachheit sei hier ein sogenanntes Fadenpendel gemeint. Für die Schwingungsdauer eines solchen Pendels gilt folgende elementare Relation (zumindest für kleine Ausschläge):

T = 2·pi·(l/g)^1/2

Dabei ist g die Erdbeschleunigung mit 9,81 m/s². Für den konkreten Pendelausschlag (Elongation) y in Abhängigkeit von der Zeit gilt dann:

y = Y·sin(phi + 2·pi·f·t)

ein physikalisches Gesetz aus: ein Zeitgesetz nämlich, den gesetzmäßigen zeitlichen Ablauf der Pendelschwingung, um es genau zu formulieren. Auch die allgemeinere Gleichung

y = f(y₀,P,t)

symbolisiert die allgemeinste Form eines Zeitgesetzes in einem einfachen System. Wesensmerkmal für Zeitgesetze ist die Zeit als unabhängige Variable! Denken wir uns jetzt ein zweites Pendel, welches mit dem ersten in irgendeiner Weise gekoppelt ist, so könnte dies entsprechend Abbildung 2 erfolgen. Die Pendelschwingungen mögen jetzt senkrecht zur Zeichenebene gedacht werden. Die Kopplung sei durch einen weiteren Faden realisiert. Dieses System soll die Wechselwirkung zweier Pendel veranschaulichen. Die dazu gehörenden Gleichungen sind etwas komplizierter und für uns nicht von Interesse. Versetzen wir die beiden Pendel in Schwingungen, so ist leicht nachzuvollziehen, dass mit einer Beeinflussung eines Pendels, indem man es beispielsweise anstößt, auch die Schwingungen des zweiten Pendels eine Veränderung erfahren. Beide Pendel können nicht mehr losgelöst vom anderen ihre Schwingungen vollführen. Sie befinden sich in Wechselwirkung. Jede Änderung an einem System ist mit der Änderung an mindestens einem zweiten System verbunden („Fall 1“).

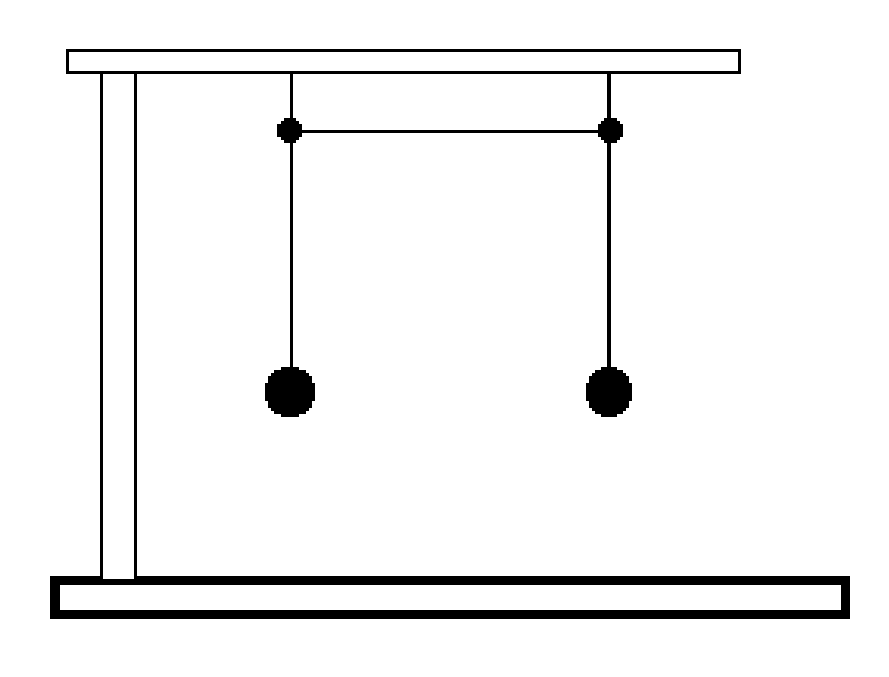Abbildung 2

y₁ = f₁(y₁₀,P,t)

y₂ = f₁(y₁₀,P,t)

Befinden sich beide Systeme in Wechselwirkung - wie im Beispiel der gekoppelten Pendel -, so brauchen wir beide Gleichungen nur geringfügig zu modifizieren („Fall 2“) und erhalten:

y₁ = f*₁(y₁₀,P₁,t,y₂)

y₂ = f*₁(y₂₀,P₂,t,y₁)

Nochmals sei betont, dass diese Darstellungsform weder einen konkreten physikalischen noch mathematischen Inhalt besitzt, sie soll nur Zusammenhänge in abgekürzter Schreibweise symbolisch darstellen. Drücken wir diese Beziehungen verbal aus, so könnte folgende Formulierung herauskommen: Der Systemparameter y₁ des Systems S₁ hängt ab von dessen Anfangswert y₁₀, den Systemkonstanten P₁, der Zeit t und - das ist jetzt neu - vom Systemparameter y₂ des Systems S₂. Analoges gilt dann auch umgekehrt für das zweite System S₂, welches in irgendeiner Form seinerseits von S₁ abhängt. Dies ist nicht anderes, als die formale Beschreibung eines Aspektes des o. g. Wechselwirkungsprinzips. Was jedoch unterscheidet den ersten vom zweiten Fall? - Der Fall 1 behandelt zwei voneinander unabhängige Systeme. Was wir mit dem zweiten System auch veranstalten, es hat keinen Einfluss auf das erste - und umgekehrt. Im Fall 2 hingegen wird jede von außen herbeigeführte Einflussnahme an einem System mit einer Reaktion des anderen System quittiert. Im Falle der beiden Pendel ist dies (auch experimentell mit geringem Aufwand nachvollziehbar) ohne weiteres einsichtig. Diese „von außen herbeigeführte Einflussnahme“ kann sein das Festhalten oder Anstoßen eins Pendels von Hand oder ein sonstiger „Umwelteinfluss“. dass wir uns so umständlich mit ausgesprochenen Trivialitäten befassen, hat einzig und allein den Grund, das „Haar in der Suppe“ zu finden. Dazu denken wir uns jetzt zwei unabhängige Pendel aufgestellt. Für diese gelten naturgemäß zwei analoge Gleichungen, die wir folgendermaßen notieren:

y₁ = Y₁·sin(phi₁ + 2·pi·f₁·t)

y₂ = Y₂·sin(phi₂ + 2·pi·f₂·t)

Nehmen wir die erste Gleichung und lösen sie nach der Zeit auf und setzen den gewonnenen Ausdruck - anstelle von t - in die zweite Gleichung ein (wer Spaß daran hat, mag dies durchführen), so haben wir formal jenen Vorgang vollzogen, den wir in der Praxis Zeitmessung nennen. Es wird nicht die abstrakte Zeit (dies ist nun einmal unmöglich; damit befassten wir uns bereits ausgiebig, vgl. Der Pygmalion-Effekt) gemessen, sondern ein Vergleich angestellt zwischen zwei - voneinander unabhängigen! - Prozessen. Der eine Prozess dabei übernimmt die Rolle einer Uhr. Eine Uhr also ist, im jetzigen Zusammenhang gesehen, ein System, in welchem ein periodischer Prozess abläuft, welcher weitgehend unabhängig sein muss von - wie auch immer gearteten - lokalen Umwelteinflüssen. Derartige Einflüsse zum Beispiel sind: Temperatur, Feuchtigkeit, mechanische Einwirkungen, elektromagnetische Beeinflussung und was sonst noch denkbar wäre. Die „astronomischen Uhren“ sind uns wohlbekannt. Jene bescheren uns zyklische Prozesse, welche wir als Zeitmaßstäbe angenommen haben, die da sind: Tag, Monat und Jahr. Da diese Einteilung im
allgemeinen zu grob ist, hat man sich feinere Maßeinheiten einfallen lassen, welche sich als Bruchteile jener „natürlichen“ Maßstäbe definieren lassen: Stunde, Minute, Sekunde. dass man heutzutage andere Zeitnormale nutzt, welche die oben aufgeführte Unabhängigkeit von lokalen Einflüssen weitgehend realisieren, sind technische Details, die für uns keine Bedeutung haben. Auch die Tatsache, dass atomare Prozesse im Bereich der Mikroobjekte (Stichwort: „Atomuhren“) unter ganz bestimmten Voraussetzungen, jene Bedingungen erfüllen, wollen wir zunächst als gegeben hinnehmen, ohne diese Tatsache interpretieren zu wollen. (Endgültig wird uns das in diesem Text auch nicht gelingen. Interessant dabei jedoch ist, die gerade genannten atomaren Prozesse bilden sowohl genaue Zeit- als auch Längenmaßstäbe.) Da uns technische und mathematische Einzelheiten nicht interessieren, betrachten wir wieder die beiden symbolischen Gleichungen.

y₁ = f*₁(y₁₀,P₁,t,y₂)

y₂ = f*₂(y₂₀,P₂,t,y₁)

Die zweite Gleichung lässt sich - zumindest prinzipiell - in folgende Form überführen, wenn wir erstere nach der Zeit t auflösen:

y₂ = F₂(y₂₀,P₂,y₁)

Die Funktion f*₂ nimmt mit Sicherheit eine andere Form an, was symbolisch durch F₂ ausgedrückt wird. Und die Rolle der Zeit übernimmt jetzt der Systemparameter y₁. Verfahren wir umgekehrt, so erhalten wir für das System S₁ ein vergleichbares Resultat:

y₁ = F₁(y₁₀,P₁,y₁) .

Betrachten wir beide symbolischen Gleichungen, so wäre der Schluss naheliegend, dass die Systeme S₁ und S₂ sich in Wechselwirkung befinden, was ja voraussetzungsgemäß nicht der Fall sein sollte. Die Schwingungen des Pendels S₁ werden nicht von den Schwingungen von S₂ beeinflusst (beziehen wir dies alles auf unseres konkretes Beispiel mit den Pendeln.) Betrachten das Ganze im Zusammenhang, so könnte man zu dem eigenartigen Schluss kommen, es gäbe echte Wechselwirkungen und solche „über die Zeit gekoppelten“. Und genau zu dieser Angelegenheit äußerte Ernst Mach sich vor mehr als hundert Jahren (E. Mach, Die Mechanik in ihrer Entwicklung, Leipzig 1933, Nachdruck: Darmstadt 1991, S. 217 f.):

Ernst Mach Wenn ein Ding A sich mit der Zeit ändert, so heißt dies nur, die Umstände eines Dinges A hängen von den Umständen eines Dinges B ab. Die Schwingungen eines Pendels gehen in der Zeit vor, wenn dessen Exkursion von der Lage der Erde abhängt. Da wir bei der Beobachtung des Pendels nicht auf die Abhängigkeit von der Lage der Erde achten zu brauchen, sondern dasselbe mit irgendeinem anderen Ding vergleichen können (dessen Zustände freilich wieder von der Lage der Erde abhängen), so entsteht leicht die Täuschung, dass alle diese Dinge unwesentlich seien. Ja wir können, auf das Pendel achtend, von allen übrigen Dingen absehen und finden, dass für jede Lage unsere Gedanken und Empfindungen andere sind. Es scheint demnach die Zeit etwas besonderes zu sein, von dessen Verlauf die Pendellage abhängt, während die Dinge, welche wir zum Vergleich nach freier Wahl herbeiziehen, eine zufällige Rolle zu spielen scheinen. Wir dürfen aber nicht vergessen, dass alle Dinge miteinander zusammenhängen und dass wir selbst mit unseren Gedanken nur ein Stück Natur sind. Wir sind ganz außerstande, die Veränderungen der Dinge an der Zeit zu messen. Die Zeit ist vielmehr eine Abstraktion, zu der wir durch die Veränderung der Dinge gelangen, weil wir auf kein bestimmtes Maß angewiesen sind, da eben alle untereinander zusammenhängen... In unseren Zeitvorstellungen drückt sich der tiefgreifendste und allgemeinste Zusammenhang der Dinge aus.... Insofern nur ein Teil der Veränderungen in der Natur von uns abhängt und von uns wieder rückgängig gemacht werden kann, erscheint uns die Zeit als nicht umkehrbar, die verflossene Zeit als unwiederbringlich vorbei... Und an anderer Stelle (A.a.O., S. 252.): Nur unsere Unfähigkeit, alles auf einmal zu übersehen, nötigt uns, wenige Körper zu betrachten und von den übrigen vorläufig in mancher Beziehung abzusehen, was eben durch die Einführung der Geschwindigkeit, welche die Zeit enthält geschieht. Man kann es nicht für unmöglich halten, dass an Stelle der Elementargesetze, welche die gegenwärtige Mechanik ausmachen, einmal Integralgesetze treten (um einen Ausdruck C. Neumanns zu gebrauchen), dass wir direkt die Abhängigkeit der Lagen der Körper voneinander erkennen. In diesem Fall wäre dann der Kraftbegriff überflüssig geworden. Auch folgende besonders wichtige Aussage geht uns an: In unsern Zeitvorstellungen drückt sich der tiefgreifendste und allgemeinste  Zusammenhang der Dinge aus.

Was haben alle genannten mechanischen Uhren gemeinsam? - Es sind rotierende (Himmelskörper) und schwingende (Uhren mit Pendel oder Unruh oder auch der Quarzkristall in einer Quarzuhr) Massen! Die bei klassischen Uhren immer beteiligten Massen sind Ausdruck der Wechselwirkung der Körper mit dem kosmischen Umfeld (Machsches Prinzip). Die beiden unabhängig schwingenden Pendel unseres Beispiels sind eben unabhängig - aber nur unabhängig voneinander. Andererseits sind sie untrennbare Bestandteile des kosmischen Umfeldes. Somit sind die „über die Zeit gekoppelten Wechselwirkungen“ so unsinnig nicht wie sie uns anfangs erschienen. Dazu nochmals zusammenfassend:

Für die klassischen Bewegungen gilt das Machsche Bezugssystem, das durch ein Inertialsystem approximiert werden kann. Die klassische Zeitmessung beruht letztendlich auf der Beobachtung mechanischer Bewegungsformen (Translation, Rotation und Oszillation), die träge Massen als hauptsächliche „zeitbestimmende Glieder“ besitzen. Die Gültigkeit der Inertialsysteme ist an bestimmte Bedingungen geknüpft.

Als Machsches Bezugssystem (1.) sei unsere Galaxis angenommen. Alle (zunächst klassischen) Zeitbestimmungen stehen mit der Trägheit und somit mit dem Mach schen Bezugssystem im Zusammenhang. Dies legt den Schluss nahe, dass allein durch die Tatsache der Korreliertheit (2.) voneinander unabhängiger Prozesse - die Zeitmessung beruht ja darauf - der Fakt folgt, dass eben alle (klassisch mechanischen) Systeme miteinander in Verbindung stehen. Dies ist jene Verbindung, die auch durch einige weiter oben aufgeschriebene Gleichungen symbolisiert wurde. Zwar befinden sich nicht die Systeme S₁ (die „Uhr“) und S₂ (der „Objektprozess“) in direkterWechselwirkung, aber sie sind Bestandteile eines in der Hierarchie übergeordneten Systems: des Machschen Bezugssystems!

Der Einfluss dieses Bezugssystems genau besteht darin, dass alle (klassisch mechanischen) Bewegungen durch „Zeitgesetze“ (s. o.) beschreibbar sind.

Aus dem Fakt des „allgemeinen allumfassenden Zusammenhanges“ der Dinge (hier im Rahmen des Machschen Bezugssystems) resultiert die Möglichkeit, all diese Prozesse annähernd so beschreiben zu dürfen, als hingen sie ab von einem einheitlichen Parameter. Und dieser Parameter ist die uns allen bekannte Zeit.

Nun war von „bestimmten Bedingungen“ (3.) die Rede, worauf wir im Hinblick auf den kinematischen Aspekt (Bahnkurve) bereits ausführlich eingegangen sind. Wie wirken sich diese Bedingungen in Sicht auf den jetzt behandelten Gegenstand, die Zeit, aus? Gibt es somit Systeme, für die der Einfluss des Machschen (kosmischen) Bezugssystems vernachlässigbar gering ist, wo dieser Einfluss um (sagen wir 39 bis 40) Größenordnungen schwächer ist als die systemspezifischen internen Einflussgrößen? - Es gibt solche Objekte in der Hierarchie der Materiestrukturen. Es sind die sogenannten Quantenobjekte, von denen wir, gesetzt den Fall, die bisherigen Überlegungen enthalten wenigstens „ein Körnchen“ Wahrheit, annehmen dürften, sie müssten ein völlig anderes als das uns vertraute Zeitverhalten aufweisen. Es läge die Vermutung nahe, die Prozesse im Bereich der Atome und Elementarteilchen könnten nicht mehr ohne weiteres an einen „äußeren Zeitmaßstab“ gekoppelt sein. Und genau jenes Verhalten zeigen bekanntermaßen und völlig „unerklärlich“ die Bausteine der Materie. Dass und wie diese Angelegenheit im Kontext mit der Kausalität zu bewerten ist, werde ich vielleicht in einem nächsten Abschnitt näher erläutern. Das scheinbar indeterministische Verhalten wurde als akausal angesehen und stand im Widerspruch zur klassischen Erfahrung. Der Ausweg bestand in der Anerkennung dieses Verhaltens als ein nur den Quantenobjekten wesenseigenen.

Aus all den bisherigen Darlegungen folgt die Einsicht in die Tatsache der Einheit von Bewegung, Zeit und Wechselwirkung. Die Schwierigkeiten in der Physik beruhen gerade auf der begrifflichen Trennung - durch Abstraktion vollzogen - dieser Gegebenheiten (vgl. Pygmalion-Effekt ). Das Nebeneinander dieser Dinge führte zu Widersprüchen, wobei bestimmte Lösungsansätze letztlich den Weg dahin wiesen, all diese Angelegenheiten nur in ihrer Einheit gelten zu lassen:

Bewegung ist Wechselwirkung; es ist nicht notwendig, letztere erst einer gedachten „wechselwirkungsfreien Bewegung an sich“ aufprägen zu müssen. Die „wechselwirkungsfreie Bewegung“ ist ein Widerspruch in sich. Der Begriff der Bewegung impliziert den der Wechselwirkung und umgekehrt.

Nochmals Ernst Mach zu diesem Thema (E. Mach, Die Mechanik in ihrer Entwicklung, Leipzig 1933, Nachdruck: Darmstadt 1991, S. 229.):

Ernst Mach Bedenkt man, dass die in die Beschleunigung eingehende Zeit selbst nichts ist als die Maßzahl von Entfernungen (oder Drehwinkeln) der Weltkörper, so sieht man, dass selbst in dem einfachsten Fall, in welchem man sich scheinbar nur mit der Wechselwirkung von zwei Massen befasst, ein Absehen von der übrigen Welt nicht möglich ist. Die Natur beginnt eben nicht mit Elementen, so wie wir genötigt sind, mit Elementen zu beginnen. Für uns ist es ein Glück, wenn wir zeitweilig unseren Blick von dem überwältigenden Ganzen ablenken und auf das Einzelne richten können. Wir dürfen aber nicht versäumen, alsbald das vorläufig Unbeachtete neuerdings ergänzend und korrigierend zu untersuchen.

Ergänzend zu diesen Gedanken gelangen wir damit zur Erkenntnis, dass unser Sonnensystem beispielsweise kein - auch nicht näherungsweise! - abgeschlossenes 10-Punkte-System (wenn nur die Sonne und die Planeten in die Betrachtung einbezogen werden) bildet. Der Fehler, den wir begehen, nehmen wir dies trotzdem an, liegt nicht in der Idealisierung, die darin besteht, sehen wir vom Einfluss weiterer vorhandener Massen ab und ist auch nicht im Modell des Masse-Punktes begründet, sondern prinzipieller Natur. Alle Bewegungen, auch die lokalen (und die Planetenbewegungen sind solche lokalen Bewegungen), dürfen wir nur im Zusammenhang zum Machschen Bezugssystem sehen. Es besteht jedoch die Möglichkeit, diese lokalen Bewegungen in ein Bezugssystem zu transformieren, welches die lokalen Beziehungen isoliert und aus dem Gesamtzusammenhang löst. Die Art und Weise, wie das geschieht, drückt unser bereits erwähntes „mechanistische Paradigma“ aus, von dem sich die Physik de facto bisher nicht zu lösen vermochte:

Das grundlegende Verständnis von der Physik ist charakterisiert durch das Nebeneinander von Raum, Zeit, Materie, Bewegung und Wechselwirkung (als Ausdruck von Eigenschaften der Objekte) sowie das Nebeneinander von vier - zunächst voneinander unabhängigen - Wechselwirkungsformen. Alle Wechselwirkungen sind von der Anlage her statischer Natur.

Der wesentliche Unterschied beispielsweise zwischen einem (freien) Neutron und dem Sonnensystem ist die Tatsache der weitgehenden Selbständigkeit des Neutrons - in Hinblick auf die interne Struktur (so man ihm eine solche zubilligt) als System - von der Umwelt im Gegensatz zum Sonnensystem, welches als fest eingebunden in das Machsche Bezugssystem gewertet werden muss.Als „massebehaftetes Teilchen“ hingegen zeigt das Neutron (wie alle anderen Elementarteilchen übrigens auch) andererseits auch seine Bindung an die kosmische Umwelt (makroskopische Eigenschaft), die dann jedoch (fast) keine Rolle mehr spielt, befindet es sich in Wechselwirkung mit „Seinesgleichen“ innerhalb der gleichen Strukturebene. Dann allerdings ist es eben kein „freies“ Neutron und erst recht kein „Teilchen“ mehr. (Auf den „Welle-Teilchen-Dualismus“ kam ich bereits zu sprechen.) Somit kann folgende Zusammenfassung formuliert werden:

Alle Umstände, die mit der klassischen Mechanik in Verbindung stehen, sind Bestandteile eines Modell-Systems. Das Koordinatensystem, die Zeit, das Trägheitsprinzip, die Kräfte usw. sind Modellgrößen, ohne - auch nicht annähernde - unmittelbare objektive physikalische Bedeutung. Die objektiven Beziehungen, aus dem Zusammenhang gerissen, zwingen uns, um der Erfahrung gerecht zu werden, diese Zusammenhänge erneut von außen herzustellen! Dieses „von außen herstellen“ drückt sich in der Tatsache der Existenz der von der Bewegung losgelösten Wechselwirkungen (Fernkräfte, Felder, Zeit etc.) aus.

Natürlich haben wir die Frage nach dem „Mechanismus“ der Wechselwirkungen nicht beantwortet, was auch noch unwichtig ist. Es geht zunächst „nur“ im die Grundhaltung, die wesentlich die weiteren Gedanken bestimmen wird. Genau so wenig konnte die Physik bisher klären, was es mit der Zeit auf sich hat und was das Wesen der bekannten „Ladungen“ ist. Und nicht beantwortete oder nicht beantwortbar erscheinende Fragen versieht man gern mit dem Etikett „irrelevant“. Es geht in diesem Text - das soll immer wieder betont werden - noch nicht um die Beantwortung bestimmter Fragen, sondern darum, sinnvolle Fragen überhaupt erst einmal zu finden und sie zu stellen.

Kommen wir jetzt auf das altbekannte Trägheitsprinzip zurück, so gilt bezüglich des räumlichen Aspektes dieses Sachverhaltes:

Ein kräftefreier Körper bewegt sich geradlinig...

Um diese Geradlinigkeit festzustellen, musste ein entsprechendes relevantes Koordinatensystem gewählt werden. Ergänzen wir den Satz in üblicher Weise:

...und gleichförmig.

„Gleichförmig“ nun heißt, „in gleichen Zeiten gleiche Strecken“ zurücklegen. Was aber bedeutet „in gleichen Zeiten“? - Dazu kommen wir wieder auf unser Beispiel mit dem Pendel zurück und notieren abermals bereits genannte Gleichung:

y = Y·sin(phi + 2·pi·f·t)

Hier handelt es sich also um einen periodischen Vorgang mit der Periodendauer

T = 2·pi· (l/g)^1/2 = 1/f

Diese Pendel ist jetzt unsere Uhr, mit deren Hilfe der Nachweis der Gleichförmigkeit einer (mechanischen) Bewegung erbracht werden kann. Nehmen wir die Periodendauer T als Zeiteinheit, so muss ein kräftefreier Körper in eben jenem Zeitintervall die jeweils gleiche Strecke zurücklegen. Sehen wir an dieser Stelle von den Schwierigkeiten ab, die mit der Bestimmung des „wahren Weges“ verknüpft sind (vgl. Das Machsche Prinzip ), so verlassen wir uns jetzt auf den Zeitmaßstab, den unsere Pendelschwingung liefert. Wir stellen auf die genannte Weise eine Verbindung her zwischen zwei Bewegungen: der Schwingung des Pendels und der kräftefreien Bewegung eines Massepunktes. Diese „kräftefreie Bewegung“ ist nach dem Verständnis der klassischen Mechanik die „wechselwirkungsfreie Grundform“ der mechanischen Bewegung überhaupt. Nach traditionellem Verständnis wird die gerade hervorgehobene Verbindung hergestellt über die Zeit.

Nun ging es doch darum, das Trägheitsprinzip verifizieren zu wollen. Ein weiterer Aspekt dieses Vorhabens ist verbunden mit der Zeitmessung. Die traditionelle Zeitmessung ist gekoppelt - in welcher Weise auch immer - an das Vorhandensein träger Massen und deren gesetzmäßiger Bewegung, welche da sein kann: Oszillation, Rotation oder auch Translation. Alle realisierbaren mechanischen Uhren nehmen ja Bezug auf jene Trägheit. Und wieder erweist der logische Kreis sich als geschlossen. (Es war auch nichts anderes zu erwarten.) Wiederholen wir Machs Auffassung, welche wir zur unseren machten:

Ernst Mach In unsern Zeitvorstellungen drückt sich der tiefgreifendste und allgemeinste Zusammenhang der Dinge aus.

Der Zeitbegriff bildete folgende Seiten objektiv realer Prozesse ab (vgl. Der Pygmalion-Effekt):

1. Veränderung
2. Periodizität
3. Irreversibilität.

Dies nun dürfen wir erweitern:

1. Veränderung
2. Wechselwirkung
3. Periodizität
4. Irreversibilität.

Da es aber die „wechselwirkungsfreie Bewegung“ nicht gibt, können wir wieder vereinfachen. Der Zeitbegriff beinhaltet:

1. Veränderung und Wechselwirkung
2. Periodizität
3. Irreversibilität

Was aber hat das Ganze zu schaffen mit den eingangs erwähnten Geschichtchen? Wir erinnern uns: Was haben der Computer und die Uhr nicht gemeinsam? - Wiederholen wir:

In einem Mikroprozessor laufen viele parallele Prozesse ab. Der alles koordinierende “Masterprozess” geht aus von einem geradezu unanständig primitiven quarzgesteuerten Oszillator.

Diesen „Masterprozess“ als herausgelösten, von der Bewegung getrennten und übergeordneten, alle sonstigen Vorgänge synchronisierenden Prozess , den genau gibt es in der Realität nicht. Auch dann nicht, wenn dieser angebliche Prozess „Zeit“ genannt wird, nach dem alle anderen Vorgänge angeblich sich zu richten haben. Von unserem Standpunkt aus betrachtet, gibt es nur die (fast) alles verbindende Bewegung der kosmischen Objekte untereinander. Alle (klassisch) mechanischen Bewegungen (und auch die Elektrodynamik muss es sein, wenngleich wir noch nicht sagen können, in welcher Weise dies gegeben ist) sind eingebettet in diesen Zusammenhang. Folgende Gegenüberstellung sind wir in der Lage, zu formulieren:

Die klassische Vorstellung stellt die Zeit als „transzendente Wesenheit“ neben die Materie und deren Bewegung. Alle Prozesse „hängen an der Zeit“ (analog zum Systemtakt im Mikroprozessor, an dem alle internen Prozesse „hängen“). Somit hängt der Verlauf aller Prozesse ab von zwei Dingen: von den Beziehungen der Objekte untereinander (Wechselwirkung) - und der Zeit. Auch hier verspüren wir ihn wieder: diesen „sanften Hauch von Dualismus“. Bewegung, Wechselwirkung und Zeit sind lediglich Teile der - durch unsere Willkür „zerhackten“ - einheitlichen Realität. Es gibt keinen von sonstiger Bewegung unabhängigen „Systemtakt“. Die Prozesse hängen nur ab voneinander und nicht zusätzlich noch von einem recht mysteriösen Ding mit der Bezeichnung „Zeit“.

dass (1.) nicht ganz der Realität entsprach, wurde bereits im Rahmen der relativistischen Theorien Einstein s deutlich. Einen noch drastischeren Hinweis auf mögliche Ungereimtheiten lieferte die Quantenmechanik und das „seltsame“ Verhalten der Mikroobjekte. Bemerkenswert ist die Tatsache, dass die ursprünglichen Fernwirkungen den Physikern seit eh und je suspekt waren. Was die „Fernwirkung Zeit“ nun betrifft, so kann man sich kaum etwas Spiritistischeres vorstellen als diese. Der Physiker aber gibt sich zufrieden, etwas messen zu können. Und die Zeit kann man messen - so scheint es. „Messen“ heißt „vergleichen“. Verglichen jedoch werden voneinander unabhängige Prozesse. Und dass dieser Vergleich zu sinnvollen Resultaten führt, ist einzig und allein und ausschließlich jener Tatsache zu verdanken, diese „Unabhängigkeit“ mit dem Zusatz „voneinander“ versehen zu müssen. Im Großen und Ganzen gibt es in Wahrheit keinen wirklich unabhängigen Prozess.

Irgendwie hängt alles zusammen. Und als einen Teil dieses Zusammenhanges lernten wir die makroskopischen Körper in Gestalt der trägen und schweren Massen kennen, welche Bestandteil des ominösen Mach schen Bezugssystems sind. Als Überleitung zu weiteren Gesichtspunkten der behandelten Angelegenheit wollen wir wieder einmal Zuflucht nehmen zu einem Gedankenexperiment, welches teilweise als Vorgriff auf noch zu behandelnde Zusammenhänge gelten kann. Wir deuteten an, dass sich die Mikroobjekte irgendwie anders (akausal und indeterministisch) verhielten. Versuchen wir hiermit eine Verbindung dieses Themenkreises herzustellen zu den bereits behandelten Fragen. Es wird beobachtet, dass ein „freies“ (ein nicht als Element eines Atomkernes existierendes) Neutron „spontan“ zerfällt in ein Elektron, Proton und ein Antineutrino. Dabei lässt sich nicht vorhersagen, wie lange ein Neutron im Einzelfall „lebt“. Genaue Aussagen aber liegen vor über die mittlere Lebensdauer einer Vielzahl solcher Objekte oder deren Halbwertzeit (Vergleichbares gilt für den radioaktiven Zerfall bestimmter Atome). Dieses nachweisliche Verhalten der angeblichen „Willensfreiheit“ jener Mikroobjekte relativierte die Auffassungen von Determinismus und Kausalität - aber speziell bezogen auf ausschließlich diese Objekte.

Stelle man sich im Gedankenexperiment vor, man könne als „transzendentes Wesen“ (um die Prozesse nicht zu beeinflussen) sich so weit verkleinern, dass man in einem Neutron Platz fände, um die genannten Prozesse vor Ort zu untersuchen, so würde man einiges mit Erstaunen feststellen: Der Zerfallsprozess liefe nach strengen Gesetzen ab. Nur, das einzelne Neutron „weiß“ (fast) nichts von seiner Umwelt. Es stellt eine für sich abgeschlossene Welt dar - mit einer eigenen „Zeit“, die (fast) überhaupt nicht mit der Zeit des Machschen Bezugssystem korreliert ist. Es findet gewissermaßen eine Abschirmung statt von genau diesem Bezugssystem, eine Abschirmung also von Gravitation und Trägheit um vielleicht 39 bis 40 Größenordnungen. Oder anders formuliert: Die Prozesse im Neutron laufen „außerhalb von Raum und Zeit ab“, jenes Raumes und jener Zeit nämlich, die durch die kosmische Inertialwelt (Machsches Bezugssystem) verkörpert wird. Der Grund dafür nun wiederum ist die Tatsache der dort um (durchschnittlich) 40 Größenordnungen schneller ablaufenden Prozesse im Vergleich zu den kosmischen Bewegungsvorgängen. Zur Vervollkommnung dieses Experiment denken wir uns tausend „Kundschafter“ der genannten Art, die tausend Neutronen untersuchen. Sie kommen alle wieder und zwar mit gleichen Versuchsergebnissen. Jedoch wann sie wiederkommen, das kann niemand voraussagen; „nur“ Wahrscheinlichkeiten lassen sich angeben. Als Halbwertzeit werden etwa 12 Minuten ermittelt. Nach 12 Minuten also sind (ungefähr) 500 Beobachter zurückgekehrt, nach weiteren 12 Minuten etwa 250 usw. Auf einen warten wir noch immer...

Dieses Gedankenexperiment enthält noch viele Ungenauigkeiten, die uns derweil nicht interessieren. Zur Veranschaulichung eines Aspektes der Statistik der Quantenobjekte aber wird es durchaus sich als nützlich erweisen. (Uns „genügen“ ohnehin qualitative Aussagen.) Wir wollen hierbei nur hervorheben, dass die „Willensfreiheit“ bestimmter Systeme, dann - und wirklich dann nur - unverständlich ist, halten wir an der Existenz eines, alle Prozesse synchronisierenden, „Systemtaktes Zeit“ fest. Die einzelnen Quantenobjekte „schauen“ eben nicht auf die „kosmische Uhr“, um festzustellen wie spät es ist. (Unser Problem wird es sein und leider auch bleiben, keine sinnvolle und in allen Punkten befriedigende Definition der Bewegung liefern zu können.)

Folgende Schlussweise ist durchaus eine angemessene:

Das Verhältnis der Stärke von Gravitation und Kernkraft beträgt etwa 1:1040. Gravitation und Trägheit sind - auch im traditionellen Sinne - zwei Seiten ein und der selben Medaille. Die klassische Zeitmessung ist an das Vorhandensein träger Massen geknüpft. Daraus folgt, dass im Bereich der Elementarteilchen der traditionell definierte Zeitmaßstab nur noch schwach an die Prozesse dieser Objekte gekoppelt sein kann. 40 Größenordnungen (im Durchschnitt) nämlich trennen die kosmische Welt von der Welt der Mikroobjekte. Es sind eben „Welten“, die beide Bereiche voneinander scheiden.

Dies ist eine recht abstrakte Argumentation, die es noch zu untersetzen gilt. Das folgende Kapitel wird sich mit einer anderen Seite der in diesem Kapitel behandelten Problematik (Als Vorgriff darauf ist das gerade beschriebenes Gedankenexperiment zu verstehen) auseinandersetzen. Dies bezieht sich auf weiter oben formulierten Satz: „Von unserem Standpunkt aus betrachtet, gibt es nur die (fast) alles verbindende Bewegung der kosmischen Objekte untereinander.“ Auf das in Klammern geschriebenen Wörtchen „fast“ soll es im folgenden ankommen.

Der Zeit-Begriff impliziert - dies sei jetzt zum Überdruss wiederholt - die Bewegung und Wechselwirkung, die Periodizität und die Nichtumkehrbarkeit wesentlicher Vorgänge.

• Warum eigentlich gibt es irreversible Prozesse?
• Was hat es mit dem Zufall auf sich?

Unbeantwortet anscheinend bleibt unsere Frage „Wieso weiß die Uhr, wie spät es ist“. Vielleicht aber sind wir der Antwort doch ein gutes Stück näher gekommen, denn eine Uhr repräsentiert einen Referenzprozess, der einen Zeitmaßstab liefert. Dieser Vergleichsprozess ist Bestandteil eines „allumfassenden Zusammenhanges“. Mit dem Wechselwirkungsproblem hätten wir auch das Zeitproblem gelöst und mit dem Bewegungsproblem das der Wechselwirkung. Doch letzte Aussage ist nun wirklich nicht neu und wurde in den verschiedensten Konstellationen bereits getroffen. Wichtig bei der ganzen Sache ist der Umstand, nicht mehr dem „Phantom Zeit“ nachjagen zu müssen. Und außerdem: Wir haben die Anzahl der Fragen minimiert. Das ist doch auch schon etwas. (Oder?) Es bliebe jetzt „nur“ noch zu klären, was eigentlich Bewegung ist. Und genau jenes Problem werden wir leider noch nicht lösen können, denn die klassische Anschauung „erklärt“ die Bewegung als „die Veränderung in der Zeit“. Und die Zeit kann nur gemessen werden an der Bewegung; die Zeit erkennen wir - nur und ausschließlich! - an der Veränderung.

Dieser logische Kreis muss durchbrochen werden! Frage: wie? - Genau an dieser Frage werden wir erst einmal scheitern. Dennoch haben wir damit einen entscheidenden Schritt getan: Erstens konnten wir eine relevante Fragestellung finden; und zweitens ist dieses Finden an das Eingeständnis geknüpft, diese Frage (noch) nicht beantworten zu können. Letzteres immerhin ist um einiges besser (und ehrlicher) als sich in uferlose Spekulationen zu verlieren. Und ein weiteres Problem müssen wir als ungelöst - und innerhalb unserer Überlegungen auch als unlösbares - Problem als gegeben leider hinnehmen: Wie sind die elektromagnetischen Erscheinungen hier einzuordnen? - Eng damit in Verbindung steht der Fakt, dass in sogenannten „Atomuhren“ ein weitgehend stabiler und - wie es auf den ersten Blick scheint - unabhängiger Zeitmaßstab realisierbar ist. Einige dieser Beziehungen werden uns noch an geeigneter Stelle beschäftigen bzw. haben uns bereits beschäftigt (Stichworte: diskrete Energiezustände in Atomen, Quanten sowie Welle-Teilchen-Dualismus).

Um den Zufall geht es im nächsten Text.

[Home] [ Seitenanfang]