Machsches Prinzip - Nur Beziehungen gelten
|
Die Tachonadel bewegt sich immer weiter. Die Autobahn ist gerade frei. Tempo 150 und noch
kein Ende. Es ist schon ein herrliches Gefühl. Bei 180 km pro Stunde - mehr gibt der Wagen nicht her - ist Schluss. Was Geschwindigkeit ist, kann jeder erfahren.
Wir nehmen sie wahr - im Auto z.B. Es ist schon ein Unterschied, ob man mit Tempo 5 oder 50 km/h auf ein Hindernis prallt. Natürlich wissen wir, dass die
Geschwindigkeit relativ ist. In einem fahrenden Eisenbahnwagen, der mit 150 km/h über die Schienen fährt, können wir gemütlich und unbehelligt auf und ab gehen,
zumindest solange der Zug weder Geschwindigkeit noch Richtung ändert. Wir gehen den Gang entlang und bewegen uns als Fußgänger so, als gingen wir auf der Straße.
Die Bewegung als solche ohne Bezug zur Außenwelt ist nicht zu spüren (Relativitätsprinzip). Aber wir nehmen die Veränderung wahr, schauen wir aus dem Fenster.
Sowie das Geräusch des fahrenden Zuges hören wir. Und die kleinen Schwankungen der Unebenheiten des Schienenstranges vermitteln den Eindruck der Besonderheit des
Zustandes der Bewegung gegenüber dem der Ruhe.
|
|
|
Die Geschwindigkeit ist definiert als die Länge des zurückgelegten Weges pro Zeiteinheit. Legt ein Auto eine Strecke von - angenommen - 50 km in
einer halben Stunde zurück, so bewegte es sich mit einer Durchschnitts-Geschwindigkeit von 100 km/h. Die Momentan-Geschwindigkeit ist auf dem
Tacho abzulesen. dass solche Angaben sinnvoll sind, bedarf keiner weiteren Erläuterung. Eine Strecke lässt sich messen und die Zeit, die man
benötigt, diese Entfernung zurückzulegen ebenfalls. An diese Selbstverständlichkeiten haben wir uns gewöhnt.
Doch gibt es weitere Bewegungen. Die Erde steht im Mittelpunkt und alles andere kreist um selbige. Die Planeten, die Sonne und die Sterne. Wie
auch anders sollte man die täglichen und jahreszeitlichen Veränderungen verstehen. Denn bewegte die Erde sich und stünde nicht still, so müssten wir dies spüren.
Natürlich ist das falsch! Natürlich gehört es heute zu den Selbstverständlichkeiten, den ausgemachten Trivialitäten des Wissens geradezu, dass dem
nicht so ist. dass dies möglicherweise falsch war aber formulierte bereits Aristarchos von Samos (310-230 v. Ch.). Diese Erkenntnis aber wurde
lange Zeit ignoriert. Es galt weiterhin das Weltbild des Aristoteles, welches von Claudius Ptolemäus (ca. 90-170) seine mathematisch vollendete Gestalt erhielt. Der Domherr Nikolaus
Kopernikus (1473-1543) beschäftigte sich mit der Fehlerbeseitigung am gültigen Kalender. Irgendwie ging es wohl auch um die Suche von Fehlern in den Arbeiten des Ptolemäus
. Dabei vielleicht (ich habe dies nicht weiter verfolgt) stieß Kopernikus auf die in Vergessenheit geratene Hypothese des Aristarchos. Dies nun war der Beginn der „Kopernik
anischen Wende“, die eigentlich bereits 1700 Jahre zuvor etwa die „Wende des Aristarchos“ hätte heißen können, welche aber - aus welchen Gründen auch immer - nicht stattfand.
Erst Johannes Kepler (1571-1630) erkannte die genaue Gestalt jener Planetenbahnen als Ellipsen, indem er die umfangreichen astronomischen Beobachtungsdaten des Tycho Brahe
(dänischer Astronom, 1546-1601) analysierte. Darum wissen wir: Die Erde - und mit ihr alle anderen
Planeten - bewegen sich auf elliptischen Bahnen um die Sonne. Diese wiederum bewegt sich - gemeinsam mit allen Fixsternen, die damit alles andere
als „fix“ sind - um das Zentrum einer Sternenansammlung, die unter dem Namen Galaxis bekannt geworden ist. Dieser letztgenannte Umlauf dauert
für unsere Sonne immerhin ca. 200 Millionen Jahre. Was die Anzahl der genannten Sterne betrifft, so ist diese Zahl - ganz standesgemäß - ebenfalls
eine „astronomische“: 100 bis 200 Milliarden (oder so ungefähr). Dieses Sternensystem seinerseits bewegt sich...
Lassen wir es genug sein. Ob und wann ein Ende dieser Aufzählung erreicht sein könnte, ist aus Sicht unseres Erkenntnisstandes ohnehin nicht
entscheidbar. (Ist dies jemals entscheidbar?) Darauf kommt es einstweilen nicht an. Wichtig beispielsweise ist die Aussage: „Die Erde bewegt sich
auf einer elliptischen Bahn um die Sonne“. Stimmt dies wirklich? - Das soll nicht der Versuch der Rückkehr zu mittelalterlichen Anschauungen
bedeuten. Vielmehr geht es um die Frage: Was eigentlich ist eine Bahn? Was ist Bewegung? - Genau diese letzte Frage werden wir nicht wirklich beantworten können.
Zwei Beispiele von Bewegungen lernten wir bereits kennen. Das eine betraf den Weg, den ein Pkw auf der Straße zurücklegt. Das Beispiel mit der
Eisen-Bahn demonstriert den Begriff der Bahn recht deutlich: Nichts anderes als der Schienenstrang könnte diese Sache besser veranschaulichen.
Hier bezieht man sich direkt auf die Erdoberfläche. Die Erdoberfläche ist das - Bezugssystem.
Auch ein Schiff legt einen bestimmten Weg zurück. Nur ist dieser so einfach nicht zu ermitteln, wie ein Weg auf der Erdoberfläche. Sich drehende
Räder, mit einer geeichten Vorrichtung verbunden, welche den zurückgelegten Weg aus der Anzahl der Umdrehungen dieser Räder bestimmt, sind
im Wasser nicht anwendbar. Letztlich läuft es auf eine zweidimensionale Ortsbestimmung - geographische Länge und Breite - hinaus. Die Methoden
dieser Positionsbestimmung bedienen sich astronomischer Methoden. Ohne auf Einzelheiten dieser Art der Navigation eingehen zu wollen, müssen
wir zumindest das Wesentliche dieses Verfahrens erkennen. Aus Uhrzeit und der relativen Lage (Winkel) eines bestimmten Sternes in bezug zur Erd
- (oder Wasser-)Oberfläche lässt sich der Standort des Schiffes ermitteln. Dieser indirekte Weg ist erforderlich, da sich ein Schiff auf einer Fläche
bewegt, die - im Gegensatz zu festen Erd-Oberfläche - alles andere ist als starr und fest. Zwei Tatsachen dabei spielen eine wesentliche Rolle:
Erstens dreht sich die Erde innerhalb von 24 Stunden um ihre Achse (darum die Zeitangabe) und zweitens bewegen sich die Sterne (darum die
relative Positionsangabe als Winkel in bezug zur Erdoberfläche) nicht.
Fast nicht.
Jedenfalls nicht in den von uns unmittelbar beobachtbaren Zeiträumen. Wieder wird ein starres - bzw. annähernd starres - Bezugssystem
herangezogen, um eine Ortsbestimmung durchführen zu können. (Die jahreszeitlichen Veränderungen ignorieren wir der Einfachheit halber.)
Bewegen wir uns mit dem Flugzeug in der Luft, so kommt lediglich eine dritte Dimension- die Höhe über der Erdoberfläche - hinzu. Auch hier ändert
sich grundsätzlich nichts an der Tatsache, starre Bezugskörper - die Erde und/oder den (annähernd) starren Fixsternhimmel - für die
Positionsbestimmung, und damit auch für die Bewegung heranziehen zu müssen. Welchen Bezugskörper auch immer wir wählen, er muss eine feste (starre) Bezugsbasis bilden.
Nachtrag 2018: Auch die sich mittlerweile einer gewissen Beliebtheit erfreuenden Navigationssysteme ändern an der grundlegenden
Problematik überhaupt nichts. Die Lage der maßgeblichen Satelliten in Bezug zur Erdoberfläche lässt sich zu jedem Zeitpunkt berechnen.
Wichtiges Bezugssystem hierbei ist die Erde selbst. Die weiteren Bahnparameter der Satelliten sind astronomische Parameter der bekannten
Art. Nichts Neues also. Neu lediglich sind die technischen Möglichkeiten der Auswertung der von den Satelliten gesendeten Funksignale auf
der Empfängerseite. Der technische Aufwand einschließlich der Berechnung der Daten ist schon beachtlich. Die Mikroelektronik macht es
möglich, die Position des Empfängers relativ zur Erdoberfläche in Echtzeit zu ermitteln.
Da aber die mathematische Behandlung der einzelnen konkreten Verhältnisse recht unübersichtlich ist, haben sich die Mathematiker schon seit
langem etwas einfallen lassen. Der Zweig der Mathematik, der sich in allgemeiner Form mit der Problematik der Ortsbestimmung befasst, heißt analytische Geometrie und ist mit dem Namen René
Descartes (1596-1650) verbunden. Die heute bekannte Gestalt erhielt die analytische Geometrie durch den Schweizer Mathematiker Leonhard Euler
(1707-1783). Und hier taucht der - für die etablierte Physik absolut
„lebensnotwendige“ - Begriff des Koordinatensystems auf. Wenn wir im folgenden diesen Begriff benutzen, so sollen damit rechtwinklige oder
kartesische Koordinatenangesprochen sein. Die Lage eines Punktes in einem solchen System wird durch Angabe dreier Koordinaten eindeutig
bestimmt. Die Astronomie bedient sich aus praktischen und traditionellen Gründen anderer Koordinatensysteme, die aber letztendlich mathematisch
den kartesischen äquivalent sind, zumal sich die verschiedenen Darstellungsformen mit Hilfe bestimmter Umrechnungsvorschriften, (Koordinaten-)Transformationen genannt, ineinander überführen lassen.
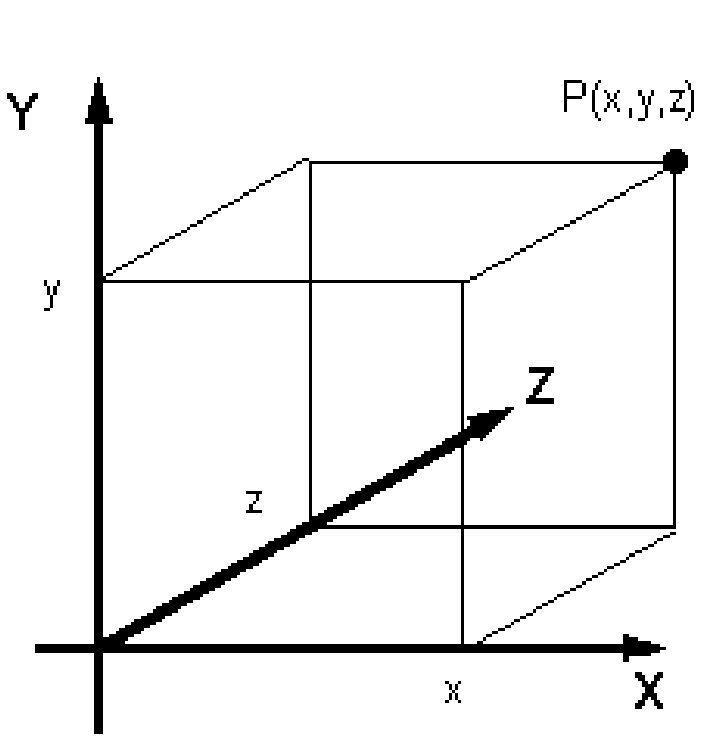 |
Abbildung 1
In wird diese Vorgehensweise prinzipiell aufgezeigt. Die Koordinatenachsen sind senkrecht aufeinander stehende Geraden und werden mit X, Y und Z
bezeichnet. Die Lage des Punktes P sei durch die Koordinaten x, y und z fixiert. Eine Bewegung dieses Punktes nun bedeutet die „Veränderung
dieser Werte in der Zeit“. Das quantitative Maß dieser Bewegung heißt Geschwindigkeit. Diese Größe kennen wir schon. Sie lässt sich im Auto
unmittelbar als Momentan-Geschwindigkeit auf dem Tacho ablesen. Die Beziehungen im Rahmen unseres Koordinaten-Systems stellen die
verallgemeinerte Form der möglichen Bewegungen innerhalb aller drei räumlichen Dimensionen dar. Dabei repräsentiert unser Koordinatensystem den dreidimensionalen Raum, der - laut Newton
- absolut und unbeweglich ist.
Verlassen wir die Erde bzw. den erdnahen Raum und bewegen uns in einem Raumschiff in eben jenem „Raum“, so wäre es durchaus interessant zu
wissen, wie hoch unsere Geschwindigkeit sei. Wie also müsste ein „Raumschifftacho“ beschaffen sein, um einen solchen Wert zu ermitteln? - Zur
Beantwortung dieser Frage verfolgen wir die Reise zurück bis zum Start des Raumschiffes. Um dem Einfluss der Erde zu entkommen, bedarf es
einer bestimmten Fluchtgeschwindigkeit. Bei der Erde beträgt sie 11,2 km/s. Auf diese Geschwindigkeit also muss eine Rakete beschleunigt werden,
um den Schwerebereich der Erde verlassen zu können. Gemeint mit dieser Geschwindigkeit ist - hier völlig eindeutig - jene „Quantität der
Bewegung“, mit der sich das Raumschiff von der Erde entfernen muss. Der Abstand Erde/Raumschiff vergrößert sich pro Sekunde um 11,2
Kilometer. Da wir aber das Sonnensystem möglichst schnell verlassen wollen, lassen wir die Triebwerke so lange arbeiten, bis wir eine
Geschwindigkeit von - sagen wir - 100 km/s erreicht haben. Diese Geschwindigkeit ermitteln wir durch den Empfang speziell zu diesem Zweck von
der Erde ausgesandter Radiosignale, deren Frequenz wir messen. Anhand der Frequenzänderung im Vergleich zur bekannten ausgestrahlten
Frequenz des irdischen Senders infolge des Doppler-Effektes lässt sich die Geschwindigkeit - im Rahmen unseres Gedankenexperimentes - leicht
ermitteln. Der „Tacho“ in diesem Fall wäre ein spezieller Radioempfänger, dessen technische Einzelheiten für uns ohne jegliche Bedeutung sind.
(Dies funktioniert anber nur in Bezug auf die Radialbewegung.)
Nachdem die Triebwerke abgeschaltet wurden, befinden wir uns im Zustand der Schwerelosigkeit. Monate sind vergangen, und wir haben uns
einige Hundert Millionen Kilometer von der Erde entfernt. Die Geschwindigkeit beträgt nicht mehr 100 km/s. Dies liegt daran, dass wir den
Einflussbereich weiterer Planeten kreuzten sowie dem ebenfalls gravitativen Einfluss der Sonne entkommen mussten. Von allem spüren wir nichts, da
die aufgeprägten Kräfte (Gravitation) immer den Reaktions-Kräften (Trägheit) entgegengesetzt gleich sind. Nur die Beobachtung der Außenwelt (In
Form der Auswertung der Radiosignale) liefert die Tatsache, uns überhaupt zu bewegen, obschon ausgesprochen langsam. Nach Jahren haben wir
auch unser Sonnensystem verlassen. Der Funkkontakt zur Erde wird immer problematischer, da die Laufzeit der Funksignale kaum noch wirkliche
Verständigung zulässt. Auch unser „Funktacho“ zeigt einen bestimmten Wert an, der noch anzeigt, wie schnell sich die Entfernung von der Erde
vergrößert. Wir sind schon so weit in „den Raum“ vorgedrungen, dass unsere Sonne ein Stern nur ist unter vielen anderen auch. Bald ist die
Funkverbindung gänzlich abgebrochen. Auch unser Geschwindigkeitsmesser quittiert seinen Dienst. Bewegen wir uns noch? - Natürlich wissen wir
das. Aber wie schnell sind wir eigentlich? - Auch diese Frage lässt sich beantworten. Dazu nutzen wir den bereits erwähnten Dopplereffekt. Jetzt
allerdings nicht mehr mit Hilfe der von der Erde ausgesandten Funksignale, sondern durch die Veränderung der Wellenlängen des von den Sternen
ausgestrahlten Lichtes. Wir peilen unsere Sonne an und bestimmen die relative Änderung der Wellenlänge (Verschiebung der Lage der Spektrallinien
im Vergleich zu einem Referenz-Spektrum.) bestimmter Spektrallinien, welche ein Maß ist für die Relativgeschwindigkeit von Sender und Empfänger
. Jetzt wissen wir, wie schnell wir uns von der Sonne entfernen - oder die Sonne sich von uns... Nur: es gibt etwa 200 Milliarden weiterer „Sonnen“
und somit eine gleiche Anzahl von Relativgeschwindigkeiten. Wir aber wollten wissen, wie schnell wir uns „durch den Raum“ bewegen.
Und dann gibt es noch Milliarden weiterer Galaxien...
Erinnern wir uns: Das „durch den Raum bewegen“, hieß im Falle des Autos „die Straße entlang fahren“. Die „Straße“ in der jetzigen Situation ist die
Flugbahn unseres Raumschiffes im Raum. Und dieser Raum nun kann durch ein Koordinatensystem bereits aufgezeigter Art dargestellt werden. Um
ein solches Koordinatensystem konstruieren zu können, jedoch bedarf es (mindestens) dreier fester Bezugspunkte. Wir aber haben 200 Milliarden
solcher - leider nicht wirklich starrer - „Punkte“ zur Auswahl. Als ersten Punkt wählen wir - als heimatbewusste Astronauten - unsere Sonne. Sie
soll den Mittelpunkt des Koordinatensystems bilden. Zwei weitere bekannte Sterne fixieren die Lage dieses Systems. Von diesen Sternen müssen
die Entfernungen untereinander und zur Sonne bekannt sein. Dank des „computergestützten Fahrtenschreibers“ ist auch unsere Entfernung zu Sonne
bekannt. Jetzt lässt sich mit Hilfe von Winkelmessungen und elementaren mathematischen Beziehungen die Lage im Raum - sprich, im gerade
definierten Koordinatensystem - bestimmen. (Diese Angelegenheit aber hat noch einen Haken, auf den wir später zu sprechen kommen.) Die
rechnerische Routinearbeit nimmt uns ohnehin der Computer ab. Das Ergebnis dieser Bemühungen ist es, jederzeit über unsere Lage und der
Bewegung „im Raum“ unterrichtet zu sein. Das Resultat wäre eine Bahnkurve, die sich sogar auf dem Computermonitor auf sehr anschauliche Weise
graphisch darstellen lässt. Diese „Kurve“ nun ist - eine Gerade. Selbstverständlich eine solche, weil wir „hinreichend weit von gravitierenden
Massen“ uns befinden. Da die Triebwerke nicht arbeiten, wirkt auf das Raumschiff keine Kraft, das sich somit - seiner Trägheit folgend - geradlinig
und gleichförmig bewegt (Trägheitsprinzip). Das Raumschiff bewegt sich in einem Bezugssystem, welches Inertial-System heißt. Jeder Physiker wird
an dieser Stelle aber lautstark Einspruch erheben, denn:
- Ein Inertialsystem ist ein Bezugssystem - durch ein Koordinaten-System repräsentiert -, in welchem das Trägheitsgesetz gilt.
- Das Trägheitsgesetz nun besagt, dass in einem Inertialsystem ein kräftefreier Körper sich geradlinig und gleichförmig bewegt.
|
|
|
Und hier haben wir ihn, den „logischen Salat“. Diese Formulierung ist nicht die willkürliche Erfindung des Autors, sondern drückt eindeutig die
Haltung der klassischen Mechanik aus. Um diesem logischen Zirkel zu umgehen, wurden ja für die Bestimmung des Koordinatensystems, in dem
sich unser Raumschiff bewegt, drei Fixsterne herangezogen. Das Problem nur war, die Sterne sind so „fix“, wie es den Anschein hat, in Wahrheit nicht
. Sie sind alles andere als feststehend. Wir erinnern uns, die Sonne bewegt sich in etwa 200 Millionen Jahren einmal um das Zentrum des
Milchstraßensystems (Interessante Frage: woran wird diese Bewegung gemessen? Dies können nur extragalaktische Objekte sein.). Dies ist schon,
innerhalb unserer Erfahrungswelt, eine recht beachtliche Zeitspanne. Damit scheint der Fehler, nehmen wir an, die Sterne bewegen sich nicht, zunächst vernachlässigbar gering.
Andere Bewegungsformen zum Beispiel sind die Planetenbahnen unseres Sonnensystems. Aus der schon riesigen Entfernung zu diesem System lässt
sich alles recht gut in dem Bordteleskop beobachten, bringt man nur die nötige Geduld auf. Immerhin 88 Tage dauert die Umkreisung Merkurs. 365
Tage benötigt unser Heimatplanet für die Umrundung der Sonne. Die Bahnen sind Ellipsen. Auch dies lässt sich mit dem Teleskop beobachten und
mit Hilfe des Computers trefflich simulieren. Was aber soll das alles? - Es ging doch darum, den Begriff der Bewegung im Raum zu erläutern. Lassen wir dies zusammenfassend formulieren:
|
Der physikalische Raum lässt sich mathematisch mit Hilfe eines dreidimensionalen Koordinatensystems beschreiben.
|
|
|
Zur Konstruktion eines solchen Koordinatensystems bedarf es starrer Bezugskörper. Mögliche Bezugskörper sind die Erde, die Sonne und/oder die
Fixsterne als „annähernd starre“ Körper.Die Fixsterne (bzw. der „Fixsternhimmel“) können nur näherungsweise als Bezugskörper dienen. Dies gilt
innerhalb der Zeiträume, in denen die Eigenbewegung der Sterne vernachlässigbar ist. Für die uns zugänglichen Zeitspannen und die meisten Sterne
gilt dies uneingeschränkt.Bei der Beurteilung der Planetenbewegungen ist die Wahl eines Koordinatensystems sinnvoll, in welchem die Sonne den
Mittelpunkt bildet. In diesem System bewegen sich die Planeten auf elliptischen Bahnen um die Sonne.
Eigentlich müsste der Massemittelpunkt des gesamten Sonnen-Systems genommen werden, was uns jedoch nicht interessieren soll. dass die
Planetenbahnen keine wirklich exakten - geschlossenen - Ellipsen sind, ist in diesem Zusammenhang ebenfalls ein unwesentliches Detail.
Für einen iminterstellaren Raum befindlichen Körper unterliegt die Wahl der Bezugskörper keinen sinnvoll begründbaren Restriktionen. D.h., die
Wahl der notwendigen drei Bezugspunkte ist willkürlich und wird durch keinerlei Zwang eingeschränkt. Es gibt - allein in unserer Galaxis - etwa 200
Milliarden potentieller Bezugspunkte. Damit haben wir ca. 1033 Möglichkeiten, ein Koordinatensystem zu konstruieren, da nur drei solcher Punkte
benötigt werden. All diese Systeme sind in Beziehung zur Bewegung unseres Raumschiffes gleichwertig. Welche Auswahlkriterien innerhalb der
klassischen Mechanik möglich sind, wird uns noch beschäftigen. Bereits gefallenes Stichwort: Inertialsystem.
Drei Bezugspunkte reichen, wollen wir korrekt sein, nicht aus, um ein Koordinatensystem eindeutig zu bestimmen, da es dann noch sechs frei
wählbare Parameter gibt, die zur eindeutigen Fixierung dienen müssen. Für die jetzigen grundlegenden Überlegungen spielen diese Dinge eine nur
untergeordnete Rolle, sodass wir uns mit diesen „Feinheiten“ nicht befassen müssen, zumal es sich um dynamisch irrelevante Fakten handelt, da
die willkürliche Festlegung der sechs Parameter keinen Einfluss auf das Geschehen hat.
Es erscheint dies alles ziemlich umständlich und überflüssig. Welche Bedeutung aber hat die Beschäftigung mit diesen hier dargelegten
Zusammenhängen innerhalb der Physik wirklich? - Physik - und hier sei zunächst von der Mechanik die Rede - beschäftigt sich mit der Bewegung.
„Bewegung“ aber heißt immer „Bewegung in bezug auf“. „Absolute Bewegung im Raum“ gibt es nicht. In der Newtonschen Mechanik ist dieser
„Bezugskörper“ - geht es um beschleunigte Bewegungen - der (hier noch absolute) Raum. Doch kann man in der Mechanik mit „dem Raum“ als
Abstraktum nicht allzuviel anfangen. Dieser Raum muss mathematisch quantitativ konkret fassbar sein. In diesem Zusammenhang lernten wir das
Koordinatensystem kennen. Die Einteilung der Erdoberfläche in geographische Längen und Breiten beispielsweise ist eine spezielle Form eines
zweidimensionalen Koordinatensystems mit krummlinigen Koordinaten.
Der nächste Abschnitt wird sich mit einigen weiteren Gesichtspunkten des wichtigen „Raumproblems“ befassen. Dabei wird festzustellen sein, dass
zwei mögliche Auffassungen einander diametral gegenüberstehen. Die erste davon - die allgemein anerkannte, mit der wir
uns gerade zum Teil auseinandersetzten - spielt eine der wichtigsten Rollen in der Physik überhaupt. (Erkenntnistheoretische Aspekte dieser
Problematik beschäftigten uns bereits im Abschnitt Der Pygmalion-Effekt.)
[Home] [Seitenanfang]
|