|
© 1998 - 2009 Wolfgang Neundorf |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
Spätestens seit Einstein werden Masse und Raum in einen mathematischen Zusammenhang gebracht. Ist es aber nicht tatsächlich so, dass dieser Zusammenhang sich bereits auf elementarerer Ebene manifestiert? |
 |
 |
 |
|
Trotzdem man allenthalben das Streben Newtons bemerkt, sein Gedankensystem als durch die Erfahrung notwendig bedingt hinzustellen und möglichst wenige auf Erfahrungs-Gegenständen nicht unmittelbar beziehende Begriffe einzuführen, stellte er den Begriff des absoluten Raumes und den der absoluten Zeit auf. MAn hat ihm dies in unserer Zeit öfter zum Vorwurf gemacht. Aber gerade in diesem Punkt ist Newton besonders konsequent. Er hatte erkannt, dass die beobachtbaren geometrischen Größen (Abstände der materiellen Punkte voneinander) und deren zeitlicher Verlauf die Bewegung nicht vollständig charakterisieren. (...) Es gibt also außer den Massen und ihren zeitlich variablen Abständen noch etwas, das für das Geschehen maßgeblich ist; dieses “Etwas” fasst er als die Beziehung zum “absoluten Raum” auf - Albert Einstein |
|
|
Die Masse - Masse und RaumDie Natur verhält sich - dies der immer noch gültige Glaube in den Naturwissenschaften - so und nicht anders wie ein technisches Systeme sich verhält, welches wir geschaffen haben. Und „die Natur“ ist das Universum, sind die Steine und Metalle, die Atome, Mücken und Elefanten. Und wir natürlich auch. Die Wissenschaften versuchen die Ursachen zu ergründen. Für alles mögliche. Die Geister und Dämonen spielen nur noch eine untergeordnete Rolle, nämlich die, dass man in der Lage ist zu beweisen, auf jene verzichten zu können. Die Wissenschaft beseitigte den Aberglauben. (Das ist wohl bekannt.) Nur an einem Aberglauben hält sie immer noch fest: dem Glauben daran, dass alles so schön einfach ist, wie wir es gerne hätten. Behauptungen aufzustellen, ist nicht besonders schwer. Schwieriger schon wird es, versucht man Behauptungen zu beweisen. Ein erster Schritt dazu wäre es, sich mit konkreten Beispielen auseinanderzusetzen. Was also liegt näher, als sich einem ganz besonders einfachen Fall zu widmen. Wer schon einmal einen schweren Koffer zu tragen hatte oder ein Auto anzuschieben versuchte, der weiß mit Sicherheit, was es mit der „Masse“ auf sich hat. Die Masse gehört zu den fundamentalen Größen der Mechanik und damit der Physik überhaupt. Und der Massebegriff bedarf keiner Erläuterung. Über den intuitiv sicher benutzten Begriff der alltäglichen Praxis und im ebenso alltäglichen Sprachgebrauch gehen die Physiker insofern nur hinaus, als dass sie ihn möglichst exakt quantifizieren und ihn in Relation zu anderen Größen setzen (der Kraft beispielsweise - je größer eine Masse, um so schwerer ist sie auch und um so schwerer lässt sie sich in Bewegung setzten oder auch abbremsen). Das alles ist so einfach und damit stinklangweilig, dass es fast schon als Zumutung erscheint, den Leser mit dermaßen trivialen Dingen zu behelligen. Doch genau jene Einstellung wird sich als völlig falsch erweisen. Dieses Kapitel wird sich mit der - noch unvollkommenen - Analyse des Massebegriffes widmen. Und dieses Kapitel ist das bis jetzt umfangreichste und wird womöglich auch gedanklich der nicht gerade besonders leicht nachvollziehbare Teil dieses Textes sein. Denn genau der Massebegriff wird eindeutig nahelegen, dass „die Welt“ nicht, ohne in allergrößte Schwierigkeiten zu geraten, in ihre „einfachen Bestandteile“ zergliedert werden darf. Und einer dieser „einfachen Bestandteile“ ist - so der immer noch gültige Glaube - die Masse. Die Masse gehört zu den SI-Basiseinheiten. Sie ist eine der fundamentalen Größen in der Physik. Intuitiv sind wir durchaus in der Lage, mit dem Massebegriff einigermaßen sicher umzugehen. (Ziel dieses Kapitels ist es, darüber nachzudenken, ob die „Masse“ wirklich eine fundamentale Größe ist, oder ob sie nicht vielleicht viel mehr als Resultat bestimmter noch unbekannter Zusammenhänge erscheint.) Unter Alltagsbedingungen sind überhaupt keine Schwierigkeiten zu erwarten. Jeder Körper ist irgendwie „schwer“ - unser Körper inklusive. Und je „schwerer“ ein Gegenstand ist, um so mehr „Kraft“ auch muss man aufwenden, um ihn in Bewegung zu setzen oder ihn von einem gegebenen Bewegungszustand abzubringen. An anderer Stelle ging ich bereits auf diese Dinge sehr ausführlich ein. Das alles steht im Zusammenhang mit den Grundfragen und den Newton schen Bewegungsgesetzen („Axiomen“) der Mechanik. Genau in diesen Gesetzen kam unter anderem eine sehr wichtige Größe vor: die Masse eben. Bisher befassten wir uns mit der Problematik der Bewegung und deren Veränderung. Dabei war festzustellen, dass die „Bewegung an sich“ (der kinematische Aspekt) immer an irgendwelche Bezugssysteme gekoppelt war (Relativitätsprinzip. - Im kinematischen Sinne ist das Relativitätsprinzip trivial, da sich Bewegung anders überhaupt nicht definieren lässt.). Die Physiker ersetzten die konkreten materiellen Bezugssysteme (z.B. die Gesamtheit der Fixsterne unserer Galaxis) durch mathematische Gebilde, „Koordinatensysteme“ genannt. Dabei nahmen die „Inertialsysteme“ eine - genau genommen - nicht begründbare Sonderstellung ein: Ein Inertialsystem ist ein Koordinatensystem, in dem das Trägheitsgesetz gilt - das Trägheitsgesetz besagt, dass in einem Inertialsystem ein „kräftefreier“ Körper sich geradlinig und gleichförmig bewegt oder sich in Ruhe befindet. Und genau die Hilfskonstruktion „Inertialsystem“ bildet die wichtigste Stütze der Mechanik. Zunächst jedoch möchte ich die ersten beiden Newtonschen Sätze wiederholen:
Bevor ich zum eigentlichen Thema (Satz 2.) komme, folgende Wiederholung: Satz 1 (und natürlich auch das 2. „Axiom“) gilt nur in einem Inertialsystem. Damit allerdings hatten wir schon einmal unsere Probleme. Entweder wir sind gefangen in einem Zirkelschluss (oder einer Zirkeldefinition), oder wir kommen nicht umhin, das wichtige Inertialsystem unabhängig vom Trägheitsprinzip zu definieren. - Entweder wir „beweisen“ immer genau das (Zirkelschluss), was wir vorher als richtig voraussetzen, oder wir müssen tatsächlich nach einem Ausweg suchen. Und der Ausweg hier hieß „galaktisches Bezugssystem“. Damit gelangten wir irgendwie zum sogenannten Machschen Prinzip. Wir dürfen aber auch den 1. Newtonschen Satz als Definition für ein Inertialsystem verwenden; dann allerdings beschreibt er kein objektives Naturgesetz, sondern führt zu einer mehr oder weniger sinnvollen Festlegung, die zunächst bestimmt, was wir unter „geradlinig“ (im Sinne der Mechanik) verstehen wollen (die Frage nach der Gleichförmigkeit greife ich an anderer Stelle auf). dass unter uns unmittelbar zugänglichen Bedingungen „Geradlinigkeit“ scheinbar unabhängig von der Aussage des Satzes 1. definiert ist, darf uns nicht darüber hinwegtäuschen, dass jene „Unabhängigkeit“ an eben ganz bestimmte und ganz und gar spezielle Bedingungen geknüpft ist, die ich bereits nannte (quasi starre Bezugssysteme). Auch das Vorhandensein starrer (fester) Körper sollte kein Grund zur Beruhigung sein. Wir müssten uns eigentlich maßlos darüber wundern, dass es Stoffe mit eindeutigen und stabilen Eigenschaften - Festkörper z.B. - überhaupt gibt. Da wir aber mit solchen „Unbegreiflichkeiten“ aufgewachsen sind, fällt uns das Staunen zunächst schwer. Allerdings kamen die Physiker gar sehr ins Grübeln, als die „Quantenhypothese“ das Licht dieser Welt erblickte. Und mit Licht hat dies tatsächlich auch etwas zu tun. Dazu später mehr. Zur Vertiefung der bisherigen Überlegungen und zu einer das Verständnis der Zusammenhänge unterstützenden Wiederholung seien folgende Skizzen (Abbildung 3 und Abbildung 4) zur Veranschaulichung der Problematik der raumbezogenen Bewegung herangezogen, wobei ich der Einfachheit halber auf die „dritte Dimension“ verzichte. (Im folgenden Text teile ich nichts wirklich Neues mit. Andere Schwerpunkte werden vielleicht gesetzt. Doch wem dies zu langweilig wird, kann die nächsten Seiten überspringen.)
Abbildung 3
Abbildung 4 Die hier im Koordinatensystem eingezeichnete Gerade dürfen wir getrost kommentarlos hinnehmen. Und wenn sich ein Körper entlang einer solchen Geraden bewegt, so erfüllt er eine der Voraussetzungen des Trägheitssatzes. Was aber gilt in dieser Skizze als Bezugssystem? - Es gibt anscheinend keines. Genau dies ist natürlich falsch. Das Bezugssystem wird durch das Blatt Papier gebildet, auf welchem die Zeichnung gedruckt wurde. Dieses Bezugssystem allerdings hat mit dem objektiv realen physikalischen Geschehen nichts, aber auch gar nichts, gemein. Dieses Bild abstrahiert von allen Dingen, die es überhaupt physikalisch sinnvoll erscheinen ließe. (Für uns absolut nicht neu.) Wenn sich also ein Körper „frei im Raum“ bewegt - was dann? - Dieses Thema behandelten wir ausgiebig. „Frei im Raum“ könnte heißen: Freie Bewegung im interstellaren Raum irgendwo zwischen den Sternen. Abbildung 4 deutet die veränderte Situation an. Dabei sollen die „Punkte“ irgendwelche Sterne (eine kleine Auswahl) symbolisieren. Und unser „Raumschiff“ bewegt sich irgendwo in dem Gewimmel „durch den Raum“. Auch sieht das auf dem Papier sehr einfach aus. Zwei Probleme allerdings haben wir. Wie gewinnen wir - erstens - aus den Beobachtungen vom Raumschiff aus diese Darstellung? Und zweitens was geschieht, wenn die anderen Massen sich im Beobachtungszeitraum bewegen? Zur ersten Frage. Vom Raumschiff aus gesehen, sind - wie auch vom irdischen Standpunkt aus beurteilt - Winkelmessungen der einzelnen Objekte untereinander durchführbar. Führen wir diese Messungen zu verschiedenen Zeitpunkten aus und vergleichen die Messergebnisse (unter der Voraussetzung, dass die Sterne nicht allzu weit entfernt sind und/oder wir „hinreichend große“ Zeitabstände wählen), so stellen wir eine Veränderung (Parallaxe) fest. Daraus nun lassen sich schließlich die Entfernungen der Sterne zu uns und auch der Sterne untereinander bestimmen. (Die wäre eine relative Entfernungsbestimmung. Für die absolute Entfernungsangabe muss mindestens ein Abstand in einer gebräuchlichen Maßeinheit bekannt sein. In der astronomischen Praxis gilt - für nicht allzu große Distanzen - als ein möglicher Referenzabstand die „Astronomische Einheit“ (AE). Dies ist der mittlere Abstand der Erde von der Sonne, rund 150 Millionen Kilometer.) Sollte die Parallaxenmethode versagen und in der astronomischen Praxis versagt sie bei der Mehrzahl aller stellaren Objekte -, so werden für die Entfernungsbestimmungen die unterschiedlichsten, sich oftmals ergänzenden, Methoden herangezogen. Diese beruhen auf einem astronomischen und astrophysikalischen Wissen, das ich nicht näher erläutern möchte, weil die Einzelheiten für uns einigermaßen unwichtig sind und nur für den Fachmann von Interesse Legt man die Lage des Koordinatensystems fest - der Mittelpunkt möge von der Sonne gebildet werden, und ein beliebiger anderer Stern fixiert die Lage einer Koordinatenachse -, so lassen sich aus den Beobachtungsdaten die Koordinaten aller anderen Sterne errechnen, unsere eigene Position mit eingeschlossen. Ob wir anschließend diese Daten in unsere Zeichnung eintragen oder deren Auswertung sowieso dem Computer überlassen, bleibt unerheblich. Absolut wichtig hingegen: Alle Koordinaten sind nur indirekt bestimmbar. Führen wir die Berechnung in beliebigen Zeitabständen immer wieder aus, so werden für uns selbst - wir bewegen uns ja - auch unterschiedliche Positionen ermitteln. Und wenn wir die Triebwerke nicht einschalten und immer hübsch Abstand zu anderen Himmelsobjekten halten, werden diese Positionen entlang einer Geraden aufgereiht erscheinen. Damit haben wir, wie bereits betont, eine Forderung des Trägheitsprinzips erfüllt. Was aber - und diese Frage ist keineswegs nur spekulativer Natur - wird aus unseren Berechnungen, wenn alle Bezugsobjekte sich im Beobachtungszeitraum merklich bewegen? Wie ließe dann sich die Flugbahn unserer Raumkapsel bestimmen? - Wir ständen vor der unmöglichen Entscheidung der Wahl der Bezugspunkte zur Konstruktion des Koordinatensystems. Wir müssten zwei Sterne unter vielen anderen auswählen, welche die Lage und die Orientierung des Koordinatensystems festlegten. Und in jedem dieser Systeme würde die Bahn unserer Raumkapsel - unter sonst gleichen Bedingungen - eine völlig andere sein. Nur keine Gerade. Diese Abweichungen von der Geraden werden jedoch immer kleiner, und schließlich vernachlässigbar klein, wenn wir alle Bezugspunkte als (annähernd) untereinander feststehend annehmen können. Und diese Annahme ist unter den uns zugänglichen Bedingungen bezüglich der Fixsterne stets gegeben. Diese Zusammenhänge habe ich hiermit ausführlich wiederholt, da sie die wichtigsten Beziehungen betreffen, auf welchem die klassische Mechanik mit ihrem raum-(koordinaten-)bezogenen Bewegungsbegriff beruht. Das beschriebene Problem ist vergleichbar mit der Wahl des Bezugssystems für die planetaren Bewegungen. Die „Kopernikanische Wende“ bestand letztlich darin, bei der Wahl eines wichtigen Bezugspunktes für das Sonnensystem die Sonne (unbeweglich) in dessen Mitte zu setzen und nicht die Erde. Dies hat den entscheidenden Vorteil, dass die Sonne ein Objekt ist unter vielen gleichwertigen Sternen der Galaxis. Jedenfalls waren, vom heliozentrischen Standpunkt aus beurteilt, die Bewegungen der Planeten aus kinematischer Sicht (eine dynamische Sichtweise in unserem Sinne gab es erst seit Newton ) wesentlich einfacher darstellbar. Es folgte sogar die Unterscheidung zwischen scheinbarer und tatsächlicher Bewegung. Die wirkliche Bewegung bezog sich auf das heliozentrische Bezugssystem; und die geozentrische Bezugsbasis führte zu scheinbaren Bewegungsabläufen. Diese Unterscheidung war auch für Newton von großer Bedeutung und ist in Hinblick auf das 2. Newtonsche „Axiom“ äußerst wichtig. Weicht die „wahre Bewegung“ von der Trägheitsbewegung (Gerade) ab, so gilt dies als Hinweis darauf, dass Kräfte wirken müssen. Die „scheinbare Bewegung“ hingegen bezieht sich lediglich auf einen subjektiven Beobachtungsstandpunkt (z.B. die geozentrische Sicht), die, ohne dass Kräfte wirken müssen, von der Trägheitsbewegung abweichen darf. Untersucht man diesen Zusammenhang jedoch gründlicher, so wie wir es eben getan haben, so erscheint die Unterscheidung von „wahrer“ und „scheinbarer“ Bewegung als willkürlich und durch keinerlei objektive Kriterien gestützt (die raumbezogene Bewegung ist immer eine scheinbare Bewegung); sie macht nur Sinn vor dem Hintergrund des „un“beweglichen Fixsternhimmels. Wir sollten uns also stets vor Augen halten, dass diese Unterscheidung dadurch - und ausschließlich dadurch - nur möglich werden konnte, weil sich die Veränderungen des Fixsternhimmels derart langsam vollziehen, dass man, ohne einen großen Fehler zu begehen, sich sogar auf den heutigen Kenntnisstand berufend, durchaus von Fix-Sternen sprechen darf. Somit benötigt die „wahre“ Bewegung eben auch das „wahre Bezugssystem“: die Gesamtheit der Fixsterne eben. (Selbst, wenn wir als Bezugsobjekte die noch viel „feststehenderen“ - extragalaktischen Objekte heranziehen, haben wir das Problem nicht gelöst, sondern nur auf eine andere Ebene der Hierarchien der astronomischen Strukturen verlagert.) Dadurch erhält - so die im vorausgegangenen Kapitel getroffene Formulierung - „absolute Relativbewegung“ einen Sinn. Und - noch eine Wiederholung - Newton sah ab von jenem Bezugssystem und ersetzte dieses durch den „absoluten Raum“. Bewegt sich nun ein „kräftefreier“ Körper geradlinig oder nicht? - Unter den gegebenen astronomischen Verhältnissen dürfen wir davon ausgehen, dass dem tatsächlich so ist, vorausgesetzt, er befindet sich in ausreichendem Abstand zu anderen Massen. Aber wir müssen uns allzeit der Grenzen dieser Darstellungsweise bewusst sein. Folgende „Prophezeiung“ sei hiermit feierlich verkündet: Die raumbezogene Bewegung (in Bezug zu einem Koordinatensystem) muss dann unweigerlich zu Schwierigkeiten führen, ist die Voraussetzung eines quasi-starren Bezugssystems nicht gegeben! Sollten irgendwann in der Physik experimentelle Befunde Hinweise für solche Schwierigkeiten erbringen, so wäre dies ein unübersehbarer Fingerzeig, spätestens dann den Bewegungsbegriff grundsätzlich zu überdenken. Und - man wird es kaum für möglich halten - um die Jahrhundertwende tauchten ernsthafte Probleme auf; und das Gebäude der Physik schien stark erschüttert. Es passte fast nichts mehr zusammen. Und - man wird es kaum für möglich halten - das Überdenken der Grundlagen der Physik fand nicht statt. Neue Vorstellungen wurden entwickelt, jedoch die alten blieben nach wie vor gültig. Der Massebegriff z.B. erfuhr eine Veränderung, doch die an diesen Begriff geknüpften Voraussetzungen waren nicht Gegenstand der Überlegungen (nicht einmal bei Einstein, und das will tatsächlich etwas heißen). Die „alte Physik“ wurde nie in Frage gestellt; sie hatte sich ja seit Jahrhunderten „bewährt“. Und als die Physik die neueren Bewährungsproben eben nicht bestand, so war dies immer noch kein Anlass, über ihre grundlegenden Begriffe auch grundlegend nachzudenken, sondern darüber nur, wie man die alten Begriffe in ein neues Korsett zwängen konnte. Bewegt sich die Raumstation um die Erde auf einer „kräftefreien“ Bahn? Offensichtlich ja, zumal in diesem Fall auch keine Möglichkeit der Kraftübertragung durch den Raum ersichtlich ist. dass man dem Augenschein aber misstrauen sollte (ich habe es ja selbst oft genug erwähnt) so wissen wir, dass es die Gravitation gibt (den Beweis dafür erbringe ich selbst, fest auf dem Stuhl vor dem Computer sitzend). Und außerdem wissen wir, dass sich ein kräftefreier Körper gefälligst geradlinig zu bewegen hat. Und die Raumkapsel auf der Umlaufbahn um die Erde ist bekanntermaßen mit Sicherheit keine Gerade - vor dem „un“beweglichen Fixsternhintergrund. Wir können uns drehen und wenden wie wir wollen, aus dem logischen Teufelskreis gibt es kein Entrinnen, zumal erstens die Alltagserfahrung uns die Tatsachen auf eine ganz bestimmte Weise interpretieren lässt und zweitens die Physik auf große Erfolge verweisen kann. Abbildung 5 zeigt, was es mit der Fliehkraft (als Trägheitskraft) auf sich hat. Ein im Kreis herumgeschleuderter Gegenstand muss „gezwungen“ werden, dieser Bewegung zu folgen. Dies erreichen wir, indem diese Masse an einem Faden befestigt ist, der dafür sorgt, dass sie nicht - der Trägheit folgend - sich auf gerader Bahn auf und davon macht. Die Bahn des Mondes um die Erde folgt auch einem Kreis; und es ist ein leichtes, die dabei auftretende Fliehkraft (die ihn aus der Kreisbahn zu drängen sucht) zu bestimmen. Diese Kraft ihrerseits muss dann aber einer ihr entgegensetzten Kraft die Waage halten. Und diese Kraft ist die Gravitation, welche die unangenehme Eigenschaft besitzt, dass dafür kein „Faden“ nachweisbar ist. Der Nachweis der Fern-Kraft Gravitation erfolgt indirekt: über die Newtonschen Bewegungsgesetze. Den direkten Nachweis für die Existenz der Schwere, den wir selbst erbringen, hat aber mit der Fern-Kraft Gravitation nichts zu tun; wir befinden uns ja im (mittel- oder unmittelbaren) Kontakt mit der Erdoberfläche. - Woran dürfen wir jetzt zweifeln?
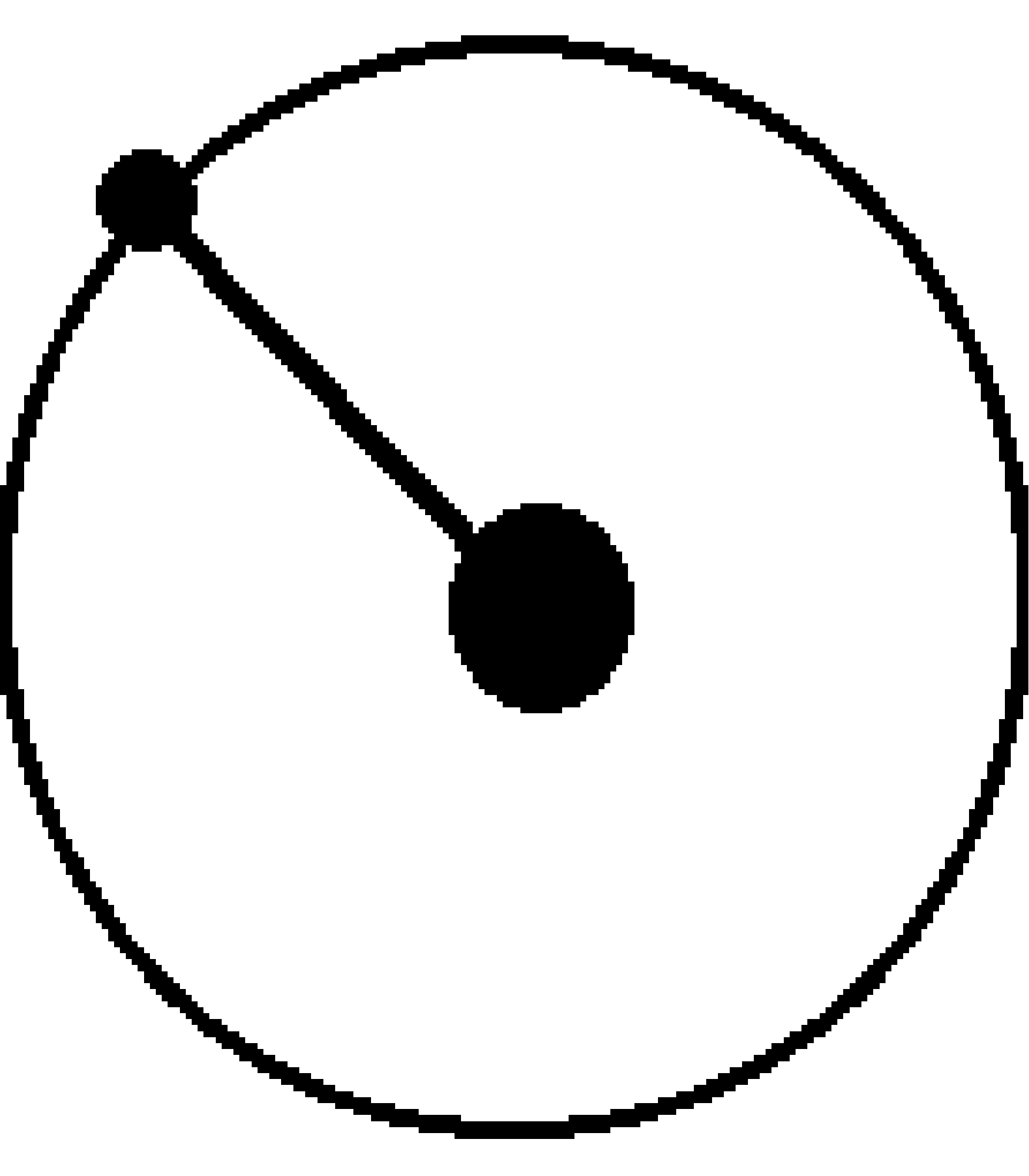Abbildung 5 Es wäre durchaus sinnvoll, daran zu zweifeln, dass durch den Raum hindurch „Kräfte wirken“ können. Dies hätte die logische Konsequenz, gleichermaßen an den Newtonschen Bewegungsgesetzen zu zweifeln, welche die Grundlage der Mechanik abgeben. Ein wichtiges Indiz dafür war die im vorigen Kapitel behandelte Gleichheit von Trägheit und Schwere. Nun gibt es leider genügend Hinweise, dass es doch „Fernkräfte“ geben müsse. Und weil sich solche Hinweise auch auf Erscheinungen berufen, die unabhängig sind von der Gravitation (z.B. elektromagnetische Phänomene), muss notgedrungen der Eindruck entstehen, dass unsere bisherigen Überlegungen jeglicher Grundlage entbehren. Irgend etwas beißt“ sich hier. Lassen wir uns jedoch von solchen Einwänden vorerst nicht beirren und ignorieren sie einstweilen. Das Ignorieren wird ja auch in der wissenschaftlichen Praxis recht erfolgreich praktiziert. Und außerdem musste selbst Einstein feststellen, dass sich Gravitation und Elektromagnetismus „beißen“; seine „einheitliche Feldtheorie“ war ihm damals nicht gelungen, obwohl er sich Jahrzehnte lang darum bemühte. Und bis in die heutigen Tage entzieht sich die Gravitation allen Bestrebungen, sie in den „Rest der Physik“ zu integrieren. Das kann kein Zufall sein. Und die mögliche Ursache ist meiner Überzeugung nach im klassischen (raumbezogenen) Bewegungsbegriff zu finden, von dem auch ein Einstein sich nicht trennen konnte. Wo also war ich stehengeblieben? - Irgendwie war die Diskussion um das erste Newtonsche Hier erweist sich die 1983 eingeführte Vorgehensweise, das Meter mit Hilfe der Lichtgeschwindigkeit zu definieren, als sehr fragwürdig, weil man auch hier wieder in einem geschlossenen logischen Kreis landen kann. Jetzt nämlich gilt die „Konstanz der Lichtgeschwindigkeit“ nicht mehr als empirisch beurteilbares Gesetz, sondern wird definitorisch festgelegt, obwohl man eben nicht weiß, in welcher objektiven Beziehung Elektrodynamik und Mechanik stehen. Es ist nicht auszuschließen, dass der Wert der Lichtgeschwindigkeit - im Vergleich zu anderen Größen - abhängig ist, von bestimmten Bedingungen, die wir eben nicht kennen. Die traditionelle Vorgehensweise betrachtet die Ausbreitungsgeschwindigkeit als fundamentale Konstante, sich dabei angeblich auf die Erfahrung stützend. Nun ist aber durchaus einzukalkulieren, dass diese Einschätzung falsch sein kann und damit der Fehlinterpretation neuer empirischer Fakten Vorschub leistet. Damit allerdings gelangen wir zum Problemkreis der „nichteuklidischen Geometrien“. Und außerdem bedient sich ja die Astronomie seit Tausenden von Jahren des Lichtes als wichtigstem Beobachtungsmittel. Ebenso bei den eben angesprochenen Problemen im Zusammenhang mit der Konstruktion eines Koordinatensystems ging ich von optischen Beobachtungen aus, dabei stillschweigend die „Geradlinigkeit“ des Lichtes voraussetzend. Die Entfernungsbestimmung mit Hilfe der Parallaxenmethode setzt die „Geradlinigkeit“ der Lichtausbreitung voraus. Auch bei der Lichtausbreitung sind wir gezwungen, diese auf ein Koordinatensystem beziehen zu müssen. Damit kommen wir auf unser bisher ungelöstes Problem zurück.) Bei der Problem-Lösung hilft uns diese Voraussetzung allerdings überhaupt nicht. Wenn wir behaupten, Licht breitet sich geradlinig aus, so ist dies eine Frage der Festlegung, nicht der empirischen Erkenntnis, denn andernfalls müssten wir „Geradlinigkeit“ unabhängig von den Eigenschaften des Lichtes definieren. Zwar komme ich anscheinend immer weiter vom eigentlichen Thema ab, doch möchte ich kurz auch auf einen anderen Sachverhalt eingehen. Wie ich bereits auseinandersetzte, versuchte Einstein einerseits das Relativitätsprinzip auch auf Nicht-Inertialsysteme auszudehnen (verallgemeinertes Realativitätsprinzip), und zum anderen wollte er der empirischen Tatsache der Gleichheit von träger und schwerer Masse gerecht werden. Als vorausgesetzte „Hintergrund-Prämisse“ galt, von der realen Existenz des Raumes nicht abzugehen. Ich erwähnte ebenfalls schon, dass „der Raum“ (oder das „Raumkontinuum“) seine mathematische Entsprechung in den Koordinatensystemen fand, wobei der Raum etwas wirklich - zunächst unabhängig von der Materie (Massen) - existentes sein sollte. Die Koordinatensysteme der analytischen Geometrie waren damit nicht nur Beschreibungs-Formen von räumlichen Beziehungen, sondern ein getreues (lineares) Abbild des real vorhandenen Raumes. Und in einem solchen Koordinatensystem (ich gehe hier lediglich auf „zweidimensionale Kontinua“ ein) wird bekanntermaßen die Angabe eines Ortes durch zwei Koordinaten bewerkstelligt. Nun bewegt sich die Mathematik selbst auf einer weitaus abstrakteren Ebene; und der Begriff des Raumes umfasst zudem völlig andere „Mannigfaltigkeiten“, als jene, die wir Durchschnittsbürger mit dem Raum in Verbindung bringen. Da gibt es beispielsweise sogenannte metrische Räume. Bei diesen Räumen ist so etwas wie ein „Abstand“ definiert (für uns eine absolute Selbstverständlichkeit). Und der Abstand zwischen zwei Punkten lässt sich aus den Koordinaten mit Hilfe ziemlich einfacher Formeln ermitteln (die ich, meinem Vorsatz gemäß, mir verkneife, zu notieren). Nur soviel: Die Vorschrift, nach der man aus den Koordinaten zweier Punkte deren Abstand errechnen kann, wird „Metrik“ genannt. Und diese Metrik ist eine konstante Größe, d.h., sie ist nicht abhängig von den Koordinaten („sie ist eine Funktion des Ortes“). Alle Räume die unserer unmittelbaren Anschauung zugänglich sind, besitzen diese einfache „euklidische Metrik“. Benannt nach Euklid von Alexandria, der etwa von 365-300 v.Chr. lebte und in seinen „Elementen“ (der Mathematik) das mathematische Wissen seiner Zeit zusammenfasste. Wesentlich dabei war seine axiomatische Begründung der Mathematik, speziell der Grundlagen der Geometrie. Axiome sind unbeweisbare Aussagen - die auf welcher Grundlage auch immer - „wahr“ sind. („Wahr“ hat in der Mathematik einen ganz anderen Sinn als in der Physik.) Auf Basis eines Axiomensystems lassen sich logische Folgerungen entwickeln, die - bei Beachtung der logischen Regeln - genau so wahr sind, wie die ihnen zugrundeliegenden unbeweisbaren Basisaussagen, dem Axiomensystem eben. Von einem Axiomensystem verlangt man mindestens, dass es widerspruchsfrei ist. Es sollte keine Aussage im logischen Widerspruch zu irgendeiner anderen Aussage stehen. (Diese Forderung erscheint trivial; die Entscheidung jedoch, ob diese Forderung in einem konkreten Fall auch tatsächlich erfüllt ist, kann im Einzelfall durchaus alles andere als einfach sein.) Desweiteren sollte ein Axiomensystem vollständig sein, d.h., die zur Verfügung stehenden Aussagen müssen für alle Schlüsse ausreichen. Es dürfen bei der logischen Ableitung von Schlüssen nicht irgendwann zusätzliche Annahmen gefordert werden, die in den Axiomen nirgends Erwähnung finden (Diese Forderung erfüllte das euklidische System in seiner ursprünglichen Fassung nicht.) Schließlich kommen wir zur Unabhängigkeit der Axiome. Alle Aussagen eines Axiomensystems müssen logisch unabhängig voneinander sein. Es sollte keine Aussage in irgendeiner Form als logische Folgerung anderer Axiome auftreten (dann wäre sie ja überflüssig). Und die Basis der euklidischen Geometrie wurde durch ein System von Grundaussagen gebildet, die (fast) all diese Forderungen erfüllten. Über die meisten Aussagen gibt es keine Diskussion. Doch das sogenannte Parallelenaxiom warf einige Probleme auf. Dabei handelt es sich um die Aussage, dass es zu einer Geraden höchstens eine zweite Gerade gibt, die durch einen nicht auf der ersten Geraden liegenden Punkt geht und die erste Gerade nicht schneidet. Diese zweite Gerade wäre dann die „Parallele“ zur ersten. Es lässt sich also zu einer gegebenen Geraden nur eine einzige Parallele konstruieren. Doch hatten sich schon vor geraumer Zeit Mathematiker (folgende Namen möchte ich kurz erwähnen: Gauß, Bólyai, Lobatschwski, Riemann) darüber Gedanken gemacht, ob dieses Parallelenaxiom durch eine andere Aussage ersetzt werden darf, und dass dann immer noch etwas Gescheites dabei herauskommt (z.B. kann es zu einer „Geraden” auch mehrere „Parallelen“ geben). Im Hinblick auf die „reine Mathematik“ waren auch solche „Geometrien“ sinnvoll. Diese allerdings weichen von dem der unmittelbaren Anschauung gegebenen Raum erheblich ab (es müssen bei der „elliptischen Geometrie“ außerdem noch weitere Axiome gegen andere ausgewechselt werden). Alles weitere sind mathematische Einzelheiten, die nicht mehr besonders leicht vermittelbar sind, und damit auch in erster Linie den Mathematiker interessieren müssen - nicht uns. Jedenfalls gelten in solchen Räumen - man hat es ja so festgelegt - völlig andere Gesetze, als im euklidischen Raum. Als Beispiel möchte ich abschließend auf die Problematik der „elliptischen Geometrie“ ansatzweise eingehen. Dazu betrachten wir als Spezialfall einer „zweidimensionalen elliptischen Geometrie“ die Kugeloberfläche. Der Mathematiker ist in der Lage, diese Fläche losgelöst von jenem dreidimensionalen Gebilde zu beschreiben, das wir „Kugel“ nennen. Es lassen sich die Eigenschaften dieser „gekrümmten Fläche“ beschreiben, ohne Zuflucht zur „transzendenten dritten Dimension“ nehmen zu müssen. Jedoch gelten auf dieser Fläche - wenn wir nur die Fläche sehen - vom üblichen abweichende Beziehungen (z.B. ist die Winkelsumme im Dreieck größer als 180 Grad). Man kann - wie auf dem Globus realisiert - ein Koordinatensystem konstruieren und damit jedem Punkt dieses „zweidimensionalen Raumes“ eindeutig Koordinaten zuordnen. Auch wird die Berechnung des Abstandes zweier Punkte aus den insgesamt vier Koordinatenangaben etwas komplizierter, zumal man ja zwei beliebige Punkte über zwei verschiedene „kürzeste Wege“ entlang eines „Großkreises“ miteinander verbinden kann. Mit den Oberflächen von rotationssymmetrischen Körpern haben wir überhaupt keine Probleme. Man kann solche Gebilde sogar unmittelbar als körperliche Modelle herstellen (für den Schulgebrauch werden im Mathematikunterricht solche Unterrichtsmittel zur Veranschaulichung herangezogen). Der Mathematiker jedoch hat ebenfalls keine Probleme damit, seine Gleichungen dahingehend zu modifizieren und zu verallgemeinern, dass auch „dreidimensionale gekrümmte Räume“ sich widerspruchsfrei beherrschen lassen. Formal gibt es keine Schwierigkeiten, einen solchen „dreidimensionalen gekrümmten Raum“ zu entwerfen, für welchen die genau bekannten Gesetze gelten . Doch der Anschauung sind solche Gebilde überhaupt nicht mehr zugänglich. Und man kann hierbei auch nicht zur „vierten Dimension“ (in Analogie zu der in die dritte Dimension gekrümmten Kugeloberfläche) Zuflucht nehmen, da der reale Raum mit drei Dimensionen auskommt, es sei denn, man sucht einen - für uns im allgemeinen unzugänglichen - Aufenthaltsort für Geister, Gespenster und die Seelen Verstorbener. Nicht zu verwechseln mit der „vierdimensionalen Raum-Zeit“ der Speziellen Relativitätstheorie, bei der formal die drei Raumkoordinaten mit der „eindimensionalen Zeitkoordinate“ unter Zuhilfenahme eines mathematischen Tricks „zusammengeschweißt“ wurden. Eine Schlüsselposition nimmt hierbei die „Konstanz der Vakuum-Lichtgeschwindigkeit“ ein. Im jetzigen Zusammenhang für uns belanglos. Die letzte Bemerkung allerdings ist gar nicht so lächerlich, wie es zunächst den Anschein hat, sondern wurde in der Blütezeit des Spiritismus im vergangen Jahrhundert von den gläubigen Akteuren (zu denen auch professionelle und anerkannte Wissenschaftler gehörten) absolut wörtlich genommen. Die Mathematik stiftete hiermit unter anderem auch einen wissenschaftlichen Eckpfeiler für Okkultismus und Spiritismus. Damit streite ich nicht über die Existenz möglicher sog. paranormaler Effekte. Dies ist ein völlig anderes Thema. Mir geht es in jetzigen Text lediglich um eine allzu naive Einstellung zu bestimmten mathematischen Erkenntnissen. Auch die moderne Physik ist kaum noch von Science Fiction zu unterscheiden. Selbst die gewagtesten Hypothesen klingen so schön wissenschaftlich. Die Mathematik und die reale materielle Welt sollte man tunlichst nicht kritik- und gedankenlos in einen Topf werfen. Dass in der wirklichen Welt auch geometrische Relationen gelten, kann und will ich nicht in Abrede stellen. Jedoch sollte man sich davor hüten, Welt und Geometrie zu identifizieren. Und dennoch kam es zu einer solchen Identifikation. Dabei muss man sich nicht einmal in die ein wenig fragwürdige Nähe der Geisterbeschwörer begeben. Die praktizierte Physik verhält sich ganz und gar nicht anders. Das allerdings ist absolut nicht lächerlich, dafür aber um so folgenschwerer. Die Kapitelüberschrift lautet - sollte dies bereits in Vergessenheit geraten sein - „Die Masse“. Und seitenlang lasse ich mich über Dinge aus, die nicht das geringste mit diesem Thema zu schaffen haben. Scheinbar nicht zu schaffen haben. Doch irgendwo ging es vorübergehend um das Thema „Allgemeine Relativitätstheorie“. Zusammenfassend möchte ich die Ausgangsposition dieser wichtigen physikalischen Theorie nochmals nennen:
Alle drei Punkte galt es, unter einen Hut zu bekommen. Und Einstein schaffte es - fast. „Fast“ hieß, die dritte Voraussetzung musste - wortwörtlich - verbogen werden. Mit den ersten beiden Sätzen hatten wir uns bereits einigermaßen ausführlich beschäftigt. Darum möchte ich den Leser von weiteren Wiederholungen verschonen. Unsere Aufmerksamkeit sei auf die dritte Aussage gerichtet. Von der in diesem Satz steckenden Grundhaltung (Realität des Raumes anerkennen) wich Einstein nie ab. (Dies hatte auch biographische Gründe, die für uns im jetzigen Zusammenhang nicht sonderlich wichtig sind.) Doch Einstein kam nicht umhin, dem Raum völlig andere und gänzlich ungewohnte Eigenschaften zubilligen zu müssen. Am besten lässt sich dies verdeutlichen, wenn ich die Aussage 3. in folgender veränderter Form niederschreibe: Nach wie vor gilt die eigenständige Realität des Raumes. Es gibt den Raum nicht nur als „Behälter für Materie“, sondern der Raum selbst stellt ein real existentes Kontinuum dar, das (dies ist die wesentliche Modifikation) nicht unabhängig von der in ihm enthaltenen Materie existiert, wobei dessen geometrische Eigenschaft (Metrik) abhängig ist von den vorhandenen Massen. Hier besann sich Einstein auf die Tatsache, dass die Mathematiker schon losgelöst von der Bedürfnissen der Physiker (die waren nicht vorhersehbar) sich mit geometrischen (und anderen) Problemen herumgeschlagen hatten, die ich gerade laienhaft anzudeuten versuchte. Und so machte er sich, auf Anregung seines ehemaligen Studienfreundes Marcel Grossmann, die geleistete mathematische Vorarbeit zunutze und versuchte - wie wir wissen, angeblich sehr erfolgreich die Gravitation als eine „Krümmung des Raumes“ zu interpretieren. „Massendichte“ und „Metrik“ waren auf ganz bestimmte Weise aneinander gekoppelt. Besagter Grossmann zeichnete auch für einen großen Teil der mathematischen Ausarbeitung und Vervollkommnung der Allgemeinen Relativitätstheorie verantwortlich. Wichtig für uns ist, dass unter der Voraussetzung des Raumes als realer Gegebenheit und unter Beachtung des Relativitätsprinzips und der Gleichwertigkeit von Trägheit und Gravitation eine Geometrie angewandt werden muss, die zwar formal beherrschbar ist, jedoch sich der direkten rationalen Erfassung grundsätzlich entzieht. Noch wichtiger aber erscheint jene Tatsache, dass die geometrischen Eigenschaften dieses Raumes von den „Massen“ abhängen sollen. Möglicherweise (ich möchte mich an dieser Stelle nicht weiter damit befassen) bringt der Einsteinsche Formalismus uns der quantitativen Beherrschung bestimmter Phänomene näher. Es erhebt sich aber die Frage, ob mit diesem Kalkül bestimmte geometrische Relationen beschrieben werden, oder ob das abstrakte Gebilde des gekrümmten Raumes tatsächlich ein unmittelbares Abbild der Realität liefert. Für Einstein gab es an der zweiten Deutung keinerlei Zweifel. Unsere Überlegungen begannen mit dem ersten Newtonschen „Axiom“ (Jetzt kann ich auch begründen, warum ich dieses Wort in diesem Zusammenhang immer mit Anführungszeichen versehe. Die berühmten Sätze Newton s erfüllen die Forderungen an ein Axiomensystem - ich nannte diese Forderungen weiter oben in diesem Kapitel - eben nicht. Ich werde mich darüber aber nicht im Einzelnen auslassen.) im Zusammenhang mit der Geradlinigkeit einer Bewegung. Nun gibt es aus der Perspektive der Einsteinschen Theorie eine solche Geradlinigkeit im allgemeinen ohnehin nicht. Ein „kräftefreier Körper“ wird sich auf der „geradest möglichen“ Bahn bewegen. Und „kräftefrei“ in diesem Sinne sind Bewegungen die ausschließlich unter dem Einfluss der Gravitation erfolgen. Seltsamerweise deckt sich das zum Teil mit unseren bisherigen Überlegungen. Erstens sahen wir auch innerhalb unserer Gedankenkette die gravitativen Bewegungen als kräftefrei an; und der Geradlinigkeit der mechanischen Bewegung galt unsere Aufmerksamkeit in gleichem Maße. Die Ausgangspositionen aber können unterschiedlicher nicht sein. Mit der Problemstrecke „Geradlinigkeit“ setzten wir uns am Anfang dieses Kapitels ausführlich auseinander. Dabei gelangten wir zu dem Schluss, dass die Sache schwierig wird, wenn wir nur ein sich veränderndes Bezugssystem zur Verfügung haben. Bei Einstein werden Massen, Raum und Gravitation irgendwie in einen Zusammenhang gestellt, in welchem der Raum (bzw. dessen Geometrie ) eine tragende Rolle spielt. Die Bewegung als solche trat vordergründig noch nicht auf. Allerdings sollten wir auf zwei Dinge nachdenklich reagieren: Erstens stellte schon Einstein eine Gleichwertigkeit von Trägheit und Gravitation fest; und zweitens hatten wir bereits den Gedanken geäußert, dass mit dieser quantitativen Gleichheit möglicherweise eine qualitativeIdentität einhergeht, die dann aber fordert, dass nicht nur die Trägheit eine dynamische Eigenschaft der Materie ist, sondern dass diese Einschätzung zudem notgedrungen auf die Gravitation ausgedehnt werden muss, auch wenn wir diese „Dynamik“ noch nicht begreifen. Hier existieren logisch zwingende Notwendigkeiten. Und wie noch gezeigt werden wird, ist die Einsteinsche Theorie ebenfalls nur unter Zuhilfenahme gekünstelter Zusatzhypothesen „nichtdynamisch“ (statisch bzw. stationär). Eine recht verworrene Geschichte wie es scheint. Und diese Geschichte wird noch undurchsichtiger, wenn ich die Frage nach der Masse stelle. Überall tauchte diese Größe auf, doch habe ich bisher noch kein Wort darüber verloren, wie diese Größe überhaupt definiert ist. Da gibt es einen sogenannten Masseprototyp, der die Masse von einem Kilogramm repräsentiert. Diese Massenormal ist ein aus einer Platin-Iridium-Legierung bestehender Zylinder, der in Sèvres bei Paris aufbewahrt wird. In allen Ländern, die das SI-System übernommen haben, gibt es Kopien von diesem „Ur-Kilogramm“ (insgesamt etwa 80 Stück, Deutschland bewahrt die Nr. 52 auf). Und diese nationalen Eichmaße werden in den dafür zuständigen Ämtern. (In Deutschland ist dies die Physikalisch-Technische Bundesanstalt (PTB) in Braunschweig.) aufbewahrt, und bilden die Grundlage für weitere hochgenaue Eichmaße. Damit allerdings gelangen wir zu dem Problem, wie man ein Original-Massestück mit einem anderen Maß vergleicht: Wie eben findet ein Massevergleich statt? - Für den Massevergleich verwendet man selbstverständlich Waagen. Und damit gelangen wir zu unserem eigentlichen Thema.
[Home] [Seitenanfang ]
|
