© 1998 - 2022 Wolfgang Neundorf
Stand: 20.08.2022

Der Begriff der Masse ist irreführend. Eigentlich dürfte nur eine Eigenschaft der “Masse”, die Trägheit nämlich, als physikalisch relevante Größe akzeptiert werden.

Die Masse - Masse und Trägheit

„Masse“ hat - so die landläufige Haltung - etwas mit „Materiemenge“ zu tun. Beginnen wir mit folgenden Sätzen, die sicherlich einleuchtend sind:

Übliche Verwendung des Massenbegriffes Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) proportional. Das Gewicht eines Körpers ist seiner Masse (Menge der Materie) proportional. Daraus folgt, dass die Trägheit eines Körpers seinem Gewicht proportional ist. (Gleichheit von träger und schwerer Masse.)

Das alles erscheint klar. Und anzunehmen ist, dass kein Physiker diesen Formulierungen widersprechen wird. Diese Aussagen zunächst sind empirischer Natur. Wie gesagt, alles ist klar - bis auf eine „völlig unbedeutende Kleinigkeit“: Was eigentlich heißt „Masse“ oder - nicht viel glücklicher formuliert - „Menge der Materie“? - Diese Frage ist äußerst leicht zu beantworten - scheint es. Dabei gehen wir vom letzten Satz aus, so dass wir nur noch uns mit dem ersten zu beschäftigen brauchen. Wir führen einen einfachen Versuch (Abbildung 6) durch. Dazu benötigen wir einen Wagen, der sich reibungsfrei auf einer ebenen Fläche bewegt. Die Skizze deutet dies an. Die Masse m sei unsere Versuchsmasse und das Gewicht soll die für die Beschleunigung notwendige Kraft K aufbringen. Gemäß dem Newtonschen 2. Axiom besteht zwischen der Kraft und der Beschleunigung eine einfache Proportionalität. Für dieses Experiment interessiert uns die Größe der Kraft nicht als absoluter Zahlenwert. Es genügt zu wissen, dass sie für unsere Versuche als konstant angesehen werden kann. Das Ziel ist es, den Satz „Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) proportional“ zu beweisen. Der Einfachheit halber nehmen wir an, die Masse des Wagens sei im Vergleich zur Probemasse verschwindend gering. Als weitere Annahme gelte, dass die “Zugmasse” (Gewicht) sehr viel kleiner sei als die eigentliche Versuchsmasse auf dem Wagen. Ansonsten gilt die hier vereinfachte Annahme, dass die Geschwindigkeit nach einer bestimmten Zeit umgekehrt proportional der Versuchsmasse ist, nicht . (Dann wäre die Geschwindigkeit reziprok proportional der Summe beider Massen. (Auf diese Ungenauigkeit wurde ich durch einen aufmerksamen Leser aus NL aufmerksam gemacht. Vielleicht werde ich hier noch eine Änderung vornehmen müssen. W. N. 03.04.2012)

 Als erste Probe nehmen wir einen Eiswürfel mit einer Kantenlänge von 10 Zentimetern. Wir bestimmen die Beschleunigung dieser Masse, indem wir die Geschwindigkeit des Wagen nach einer bestimmten Zeit ermitteln (bei konstanter Kraft ist auch die Beschleunigung konstant und damit die Geschwindigkeit linear abhängig von der Zeit) und nehmen diese Größe als Basis für weitere Vergleiche.

Dem beschriebenen Würfel ordnen wir willkürlich die „Massezahl 1“ zu. Jetzt stellen wir einen zweiten Würfel auf den ersten. Das Ergebnis ist die halbe Endgeschwindigkeit des Wagens und mithin die doppelte Masse. Um ganz sicher zu sein, halbieren wir einen dieser Würfel und wiederholen den Versuch in bekannter Weise. Natürlich erhalten wir die doppelte Endgeschwindigkeit, was einer Halbierung der Masse gleichkommt. „Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) proportional“ hätten wir somit bewiesen, da mit „Menge der Materie“ leicht das Volumen (hier das des Würfels) auszumachen ist. Das Problem wäre damit gelöst - wenn es nicht noch andere Materialien gäbe außer Wasser (der Bequemlichkeit halber wählte ich es für unser Gedankenexperiment in gefrorener Form). Versuchen wir es jetzt mit einem anderen Stoff und nehmen einen Bleiwürfel gleichen Volumens zur Hand. Die dieser Masse erteilte Beschleunigung beträgt, im Vergleich zu der mit unserem Normal erzielten, nur etwa das 0,0885-fache. Die Masse somit ist 1/0,0885 = 11,3 mal größer als die des Eiswürfels.

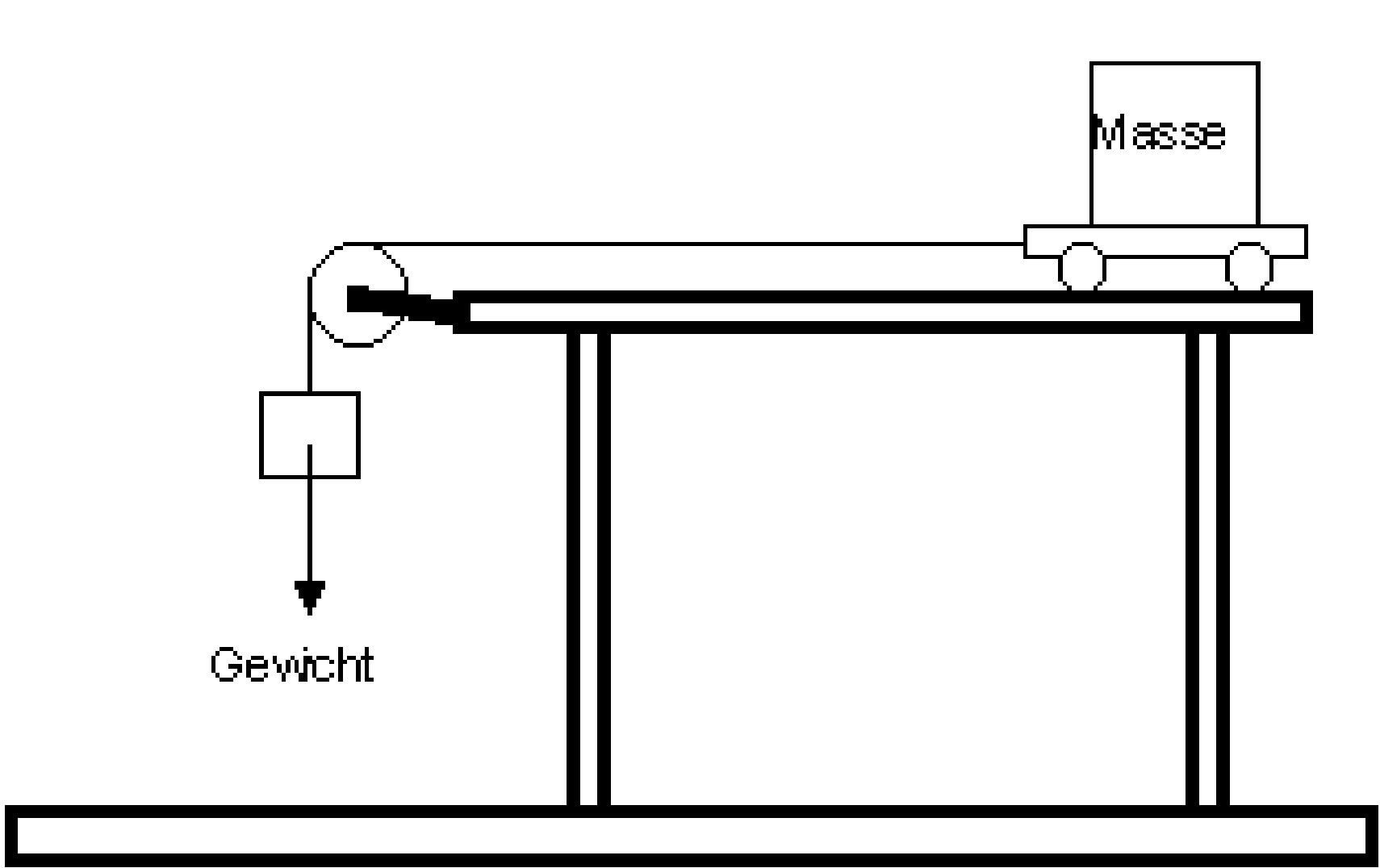Abbildung 6

Jetzt wollen wir - als unverbesserliche „Nachfrager“ - die Frage danach stellen, was wir eigentlich gemessen haben. Wir messen die Größe, die wir (Massen )Trägheit nennen. Und außerdem stellen wir fest, dass jene Trägheit der „Menge der Materie“ (hier dem Volumen) proportional ist. Die traditionelle Physik aber verwandelt diese objektive Proportionalität stillschweigend - und völlig ungerechtfertigt, wie wir noch sehen werden - in eine Identität! Es wird eine Eigenschaft (Trägheit) der Materie gleichgesetzt mit deren Quantität (Menge). Erkennen wir nur an, was wirklich prinzipiell messbar ist, dann müssen wir passen, wird uns die Aufgabe gestellt, die Masse zu bestimmen. Infolgedessen erhebt sich die Frage, welche Bedeutung der Massebegriff tatsächlich hat, oder welche Konsequenzen es hätte, Masse und Trägheit nicht gleichzusetzen.

Die Masse ist dem Volumen eines Körpers proportional. Darüber brauchen wir nicht zu diskutieren. Welcher Körper besitzt die größere Masse: ein Kubikdezimeter Wasser oder das gleiche Volumen Blei? - Die Antwort habe ich bereits gegeben. Das Blei besitzt eine um den Faktor 11,3 - dies ist dessen „Dichte“ - größere Trägheit. Ist aber das Verhältnis beider Massen das gleiche? - Ist man ehrlich, so lässt sich diese Frage überhaupt nicht beantworten, da wir etwas messen müssten, ohne dafür eine Messvorschrift angeben zu können. Denn die Definition der (Massen-)Dichte setzt die der Masse voraus; und gemessen haben wir die Trägheit. (Newton definierte die Masse u.a. als das Produkt von Dichte und Volumen, was natürlich nur dann sinnvoll wäre, könnten wir die Dichte unabhängig von der Masse definieren. Die logischen Zirkel lauern überall! Und schon Ernst Mach hatte auf diese Ungereimtheit hingewiesen.)

Versuchen wir jetzt, dieses Problem aus atomistischer Sicht zu entscheiden. „Menge der Materie“ könnte heißen, „Anzahl der Atome“. Dies gilt für die Atome eines Elementes mit Sicherheit, ist aber auch nicht völlig korrekt, da es verschiedene Isotope geben kann. Wie aber vergleichen wir Wassermoleküle mit Bleiatomen? - Ganz einfach, indem wir die Atome zählen bzw. deren Bestandteile (angenommen dieses Zählen wäre wirklich einfach). Im wesentlichen bestehen Atome aus Protonen und Neutronen (im Atomkern) und den Elektronen in der Atomhülle.

Das Mol als Mengeneinheit des Stoffes beruft sich auf bestimmte Zusammenhänge, die ich nicht im Detail erläutern will. Als Basiseinheit dafür dient die „absolute Atommasse“, die als ein Zwölftel der Masse des Kohlenstoffisotopes ¹²C definiert ist. Die so gewonnene Referenzmasse beträgt etwa 1,67·10^-24Gramm. Oder anders herum formuliert: 6,02·10²³ Kohlenstoffatome bringen 12 Gramm auf die Waage. Oder 12 Gramm Kohlenstoff ¹²C bilden die Stoffmenge von einem Mol. Die Menge eines bestimmten Stoffes in Mol ergibt sich aus der relativen (bezogen auf die eben genannte Basiseinheit) Atom- bzw. Molekularmasse in Gramm. Die Wasserstoffmenge von einem Mol besitzt die Masse von 1,008 Gramm. Und hierbei stoßen wir auf das Problem, die relativen Atommassen aller möglichen Atome zu bestimmen. Nur: bei der angeblichen Masse-Bestimmung handelt es sich immer um einen Trägheits-Vergleich oder Gewichts-Vergleich!

Die Photonen als „Quanten des elektromagnetischen Feldes“ zählen wir nicht mit, da sie erstens nicht als Bausteine zu bewerten und zweitens nicht masselos sind. Dass dies nicht ganz stimmt, werden wir noch in einem anderen Zusammenhang zu beachten haben, denn die Photonen sind zwar trägheits- aber nicht masselos, verstehen wir unter „Masse“ die Existenz von Materie. Jedenfalls existieren sie.)

Wie aber vergleichen wir die Masse des Protons mit der des Elektrons? - Diese Aufgabe kann als gelöst betrachtet werden. Informiert man sich aber darüber, wie diese „Masse“-Bestimmung erfolgt, so wird man feststellen, dass die Physiker immer - mit welch ausgeklügelten Versuchsanordnungen dies auch im Einzelfall durchgeführt wird - die Trägheit der genannten „Teilchen“ ermitteln (oder das Verhältnis von Ladung zu Trägheit). Wir kommen also auf diese Weise auch nicht unserer Aufgabenstellung näher. Das Problem wurde nicht gelöst, sondern nur verlagert und dessen Lösung hinweggeschoben.

Vielleicht aber finden wir dennoch eine Lösung, die wir in einfacher Weise zumindest auf gasförmige Medien anwenden dürfen. Da gibt es ein Gesetz, das sogenannte Avogadrosche Gesetz, (Amadeo Avogadro, italienischer Physiker, 1776-1856, siehe Bild) das besagt, dass im gleichen Volumen bei gleichem Druck und gleicher Temperatur die Anzahl der Gasmoleküle bei allen Gasen gleich ist. Bei Edelgasen gibt es naturgemäß nur Atome, deren Anzahl mit der Anzahl der Moleküle in anderen Gasen gleichgesetzt werden kann. Diese Zahl beträgt bei normalem Druck und 0°C für ein Liter Gas etwa 2,7·10²² Partikeln. Dies ist die, auf Gase angewandte, Loschmidtsche Zahl (Joseph Loschmidt, österreichischer Physiker, 1821-1895).

Abbildung 7

Nehmen wir als Beispiel zwei Gase: Wasserstoff und Helium. In einem Liter Wasserstoff befinden sich die gleiche Anzahl Wasserstoff-Moleküle wie in dem Liter Helium Helium-Atome unter den gleichen Bedingungen vorhanden sind. Bekanntlich (Ich setzte diese Dinge ganz einfach einmal als bekannt voraus. Und außerdem genügt ein ganz grober Überblick. - s. Abbildung 7) besteht ein Wasserstoffatom im allgemeinen aus einem Proton und einem Elektron. Dies ist das einfachste Atom überhaupt. „Im allgemeinen“ impliziert: Es gibt Ausnahmen. Eine solche Ausnahme bildet jenes Wasserstoffisotop, welches im Atomkern „unnützerweise“ zusätzlich ein Neutron enthält und „Deuterium“ genannt wird. Das Heliumatom seinerseits besteht im Kern aus zwei Protonen plus zwei Neutronen. Und um diesen Kern kreisen (ich verwende hier einmal diese angeblich veraltete „volkstümliche“ Formulierung) im Normalfall zwei Elektronen. Folgende Reaktion ist denkbar: Wir nehmen zwei Deuteriumkerne und „schießen“ sie zusammen, und wenn wir Glück haben, erhalten wir einen Heliumkern.

So einfach ist das Ganze nun auch wieder nicht, doch wurde es schon praktiziert. „Wasserstoffbomben“ heißen die Objekte im Volksmund, in denen eine „Kernverschmelzung“ oder „Fusion“ oder „thermonukleare Reaktion“ auf unkontrollierte und verheerende Weise vonstatten geht. Und die Sterne - so die Schulwissenschaft - „leben“ von diesem Prozess seit Milliarden von Jahren, wenngleich hier dieser Vorgang sich auf Umwegen vollzieht (hierbei handelt es sich um den sogenannten „Kohlenstoffzyklus“ und/oder die „Proton-Proton-Kette“).

Folgende einfache Milchmädchen-Rechnung gilt: Ein Heliumatom besitzt die doppelte Masse (vgl. Abbildung 7) der eines Deuteriumatoms. Eindeutiger geht es nicht. Machen wir die Probe aufs Exempel. Da die gesteuerte Kernfusion im Labor zur Zeit noch ein wenig problembehaftet ist (man arbeitet seit Jahrzehnten heftig daran) nehmen wir ganz einfach einen Liter Deuteriumgas und einen Liter Heliumgas. Beide Gasmengen enthalten die gleiche Anzahl Moleküle bzw. Atome. Da das Helium-Atom die gleiche Masse besitzt wie ein aus zwei Atomen bestehendes Deuterium-Molekül (nochmals Abbildung 7) kann man folgende Aussage treffen: Beide Gasmengen besitzen die gleiche Masse!

Dies ist eine Aussage, die wir nicht zu überprüfen brauchen, da sie durch Definition gilt. Weil wir aber sicher gehen wollen, bestimmen wir das Gewicht beider Gase (oder deren Trägheit, sind sowieso identisch). Mit Bestürzung stellen wir einen „Fehler“ fest. Das Helium wird mit etwa 99 ,27 % des zu erwartenden Gewichtes als zu leicht befunden, denn 0,73 % Prozent sind „verschwunden“. Was ist verschwunden? Masse wohl nicht (diese Aussage bedarf noch der Korrektur), aber der Trägheitswiderstand (oder das Gewicht) von einem Liter Helium ist fast ein Prozent niedriger als es seiner Masse nach sein dürfte. Der Physiker spricht vom „Massen-Defekt“.

Was schließen wir daraus? - Die Masse ist - vereinbarungsgemäß - eine additive Größe. Bei gegebener homogener „Dichte“ ist die Masse bei makroskopischen Körpern dem Volumen proportional und bei den mikroskopischen Objekten der Anzahl der Bestandteile. Zwei Säcke Kartoffeln sind eben doppelt so viel Kartoffeln wie ein Sack. Und die Trägheit ist es - erfahrungsgemäß - nicht immer.

Auf unser Beispiel mit den Kartoffelsäcken bezogen trifft dies zu, aber nicht mehr bei dem aus zwei Deuteriumkernen gewonnen Heliumkern. Doch unser Heliumbeispiel hat noch einen Haken. Um aber das Verwirrspiel nicht auf die Spitze zu treiben, wollen wir uns um jenen „Haken“ erst in einem späteren Kapitel kümmern.

Kommen wir nochmals auf das 2. Newtonsche Bewegungsgesetz zurück, welches lautet: Für jede Änderung des Bewegungszustandes (Beschleunigung) muss eine Kraft aufgewendet werden. Kraft und Beschleunigung sind (im klassischen Fall) einander proportional. Der Proportionalitätsfaktor heißt „träge Masse“ oder „Trägheit“. Jetzt schreibe ich drei - fast - identische Sätze auf:

1. Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) proportional.
2. Die Trägheit eines Körpers ist (auch) seiner Masse (Menge der Materie) proportional.
3. Die Trägheit eines Körpers ist (nur) seiner Masse (Menge der Materie) proportional.

Der erste Satz (1.) ist uns wohlbekannt. Damit fing unser Problem an. Die Sätze 2. und 3. sind - anscheinend unwesentliche - Modifikationen des ersten Satzes. Die Unterschiede betreffen die in Klammern geschriebenen Wörtchen „auch“ bzw. „nur“. In Klammern geschrieben wurden sie, weil - jedenfalls auf 3. bezogen - dieses Wort zwar stillschweigend gedacht, nie aber ausgesprochen wurde. Die Ergänzungen „auch“ oder „nur“ sind vollkommen unwichtig - scheinbar. Für die klassische Mechanik gilt der Satz 3., den wir - aufgrund von „nur“ und sinnvoll gewählten Einheiten - auch folgendermaßen notieren dürfen:

3*. Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) gleich.

Wenn aber 3*. gilt - und dies ist die seit Newton praktizierte Handhabung des Massebegriffes -, so haben wir das Problem der eigentlichen Massebestimmung (vgl. unsere weiter oben beschriebenen vergeblichen Bemühungen) anscheinend gelöst (dies ist die Newtonsche Lösung). Dann aber drückt das zweite Newton sche Bewegungsgesetz keine objektive - von uns und unserem Wissen unabhängige - Gesetzmäßigkeit aus, sondern dient der Definition der Trägheit und damit der Masse. Dann jedoch ist „Masse“ nichts als ein anderes Wort für „Trägheit“, die aber eine dynamisch definierte Größe ist. Und genau dies ist die geschichtlich begründete und praktisch gehandhabte Verfahrensweise, die uns nicht einmal einen ganz kleinen Schritt weiter bringt, denn dann benötigten wir das Wort „Masse“ überhaupt nicht mehr, weil es keine Beziehung hat zu dem ursprünglichen und historisch entstandenen Massebegriff. Auch die Massedefinition auf Grundlage eines Masseprototyps (vgl. vorausgegangene Ausführungen) bringt uns nicht weiter, da der Vergleich einer zweiten Masse mit diesem Normal unter Zuhilfenahme einer Präzisionswaage der Vergleich der Gewichte beider Massen ist. Und wenn wir von der Idendität von Schwere und Trägheit ausgehen, so haben wir damit einen indirekten Vergleich der Trägheit zweier Massen angestellt.

Bringen wir unsere Überlegungen in Verbindung zur Problematik der Inertialsysteme, so müssten wir vorher das Problem lösen, ein von dynamischen Voraussetzungen - eben von der gerade behandelten Beziehung - unabhängiges Inertialsystem zu definieren. (Ein Teilproblem des Inertialsystems - die Problematik der Geradlinigkeit einer Bewegung - behandelte ich ja nochmals im ersten Textabschnitt dieses Kapitels.) Erst wenn das gelänge, würde die gerade beschriebene Definition einen objektiven Sinn erhalten.

Nun könnte man einwenden, dies sei der physikalische Schnee von vor 300 Jahren. (Selbst dann aber hätte dieser „Schnee“ fatale Folgen.) Die Physik hat Fortschritte gemacht. Das hat sie auch. Einen dieser Fortschritte betrifft angeblich die Spezielle Relativitätstheorie. Daran geknüpft sind bestimmte Konsequenzen. Eine Konsequenz ist die „empirisch gesicherte Abhängigkeit der Masse von der Geschwindigkeit“. (Jetzt wäre noch zu untersuchen, ob es sich dabei um eine „relativistischen“ oder einen dynamischen Effekt handelt. Im Sinne meiner bisherigen Ausführungen kann es sich nur um einen dynamischen Effekt handeln, welcher sich auf das „Machsche Bezugssystem“ bezieht.)

Kein Teilchenbeschleuniger würde auch nur den Bruchteil einer Sekunde funktionieren, entspräche dies nicht den Tatsachen. Für kleine Geschwindigkeiten bleibt dieser „relativistische Effekt“, wegen des großen Wertes der Lichtgeschwindigkeit vernachlässigbar gering, da sich der „relativistische Massezuwachs“ erst bei Geschwindigkeiten bemerkbar macht, die mit der Lichtgeschwindigkeit vergleichbar ist. Dies schließt den Fakt ein, dass „normale“ Körper nie diese Geschwindigkeit erreichen können, weil ihre Masse in diesem Fall unendlich groß werden würde. Dieser Sachverhalt lässt sich folgendermaßen interpretieren: Jede Energieübertragung - (kinetische) Energie und Bewegung sind eng aneinander gekoppelt - ist untrennbar mit einer Masseübertragung verbunden. Dies gilt als ein Ergebnis der Speziellen Relativitätstheorie oder: Die Spezielle Relativitätstheorie ist in der Lage, jenen Effekt richtig zu deuten.

So scheint es!

Die letzte Formulierung jedoch erscheint lediglich als logische Folge der bereits bekannten Aussage „Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) gleich “. Gehen wir jedoch von der Aussage aus „Die Trägheit eines Körpers ist (auch) seiner Masse (Menge der Materie) proportional “, so müssen wir, wohl oder übel, die relativistische Relation des „Massezuwachses bei Bewegung“ umformulieren. Dann sind wir lediglich in der Lage, festzustellen, dass die Trägheit abhängig ist von der Geschwindigkeit - nicht die Masse!

Beide Sichtweisen beschreiben formal den gleichen quantitativen Sachverhalt. Ihre qualitativen Bedeutungen jedoch sind so unterschiedlich wie wir sie uns unterschiedlicher überhaupt nicht denken können!

Die erste Deutung betrachtet die Geschwindigkeitsabhängigkeit der Masse. Sie führt zur Aussage: Jede Energieübertragung ist untrennbar mit einer Masseübertragung verbunden. Oder: Energie hat Masse. Oder: Energie ist Materie - Materie ist Energie. Oder auch: Energie und Masse sind zwei unterschiedliche Erscheinungsformen der Materie. Dies genau entspricht der Deutung des Effektes innerhalb der Schulphysik.

Eine konkrete Konsequenz dieser Tatsache findet sich in der Verfahrensweise der Physiker, nicht nur die Energie, sondern auch die Masse der Elementarteilchen in der Maßeinheit Elektronenvolt anzugeben, wobei ein Elektronenvolt (1 eV) die Energieänderung ist, die ein elektrisch geladenes Teilchen erfährt, durchläuft es die Potentialdifferenz von einem Volt. Und in den Teilchenbeschleunigern werden auf diese Weise aus Energie - aus Bewegung also - munter neue Teilchen „erzeugt“. Auf dieses Thema komme ich an anderer Stelle nochmals kurz zu sprechen.

Die zweite Deutung jedoch besagt lediglich, dass die Trägheit abhängig ist - unter anderem auch - von der Geschwindigkeit. Dieser Zusammenhang ist anscheinend empirisch gut gesichert, jedenfalls bei elektrisch geladenen Teilchen. (Die Trägheit eines Körpers ist somit von seiner Masse und seiner Energie abhängig.)

Energie ist eine Eigenschaft der Materie und die Trägheit eine Eigenschaft der Masse. Aus der Gleichsetzung von Masse und Trägheit folgt logisch die Gleichsetzung von Materie und Energie. Eine Eigenschaft wurde damit „materialisiert“!

Nochmals: Die klassische Betrachtungsweise identifiziert die Trägheit mit der Masse in der Weise, dass „Masse“ der primäre, unabhängige und fundamentale Begriff ist und die Trägheit die sekundäre dynamische Eigenschaft der Masse. Wir erhalten zusammenfassend folgende Schlußweise:

1. Die Trägheit eines Körpers ist seiner Masse (Menge der Materie) gleich. - Historisch bedingte und beibehaltene grundlegende Einstellung, durch die Alltagserfahrung nahegelegt, von Newton wissenschaftlich kultiviert.
2. Die Trägheit einer „Masse“ hängt ab von deren Geschwindigkeit, jedenfalls dann nachweisbar, ist diese Geschwindigkeit mit der des Lichtes vergleichbar. - Empirisch gestützte Gesetzmäßigkeit neueren Datums.
3. Weil voraussetzungs- und gewohnheitsgemäß 1. gilt, und 2. als gesicherte Erfahrungstatsache akzeptiert werden muss, folgt: Die Masse ist abhängig von der Geschwindigkeit.

Da man 2. nicht ignorieren kann, aber an 1. festhält folgt 3. - und nur dann! Die Trägheit also hängt - über den logischen, historisch bedingten, Umweg Masse - ab von der Geschwindigkeit.

Lösen wir uns von der historisch entstandenen Newtonschen Prämisse und dem genannten logischen Umweg, so bildet die Aussage „Die Trägheit ist abhängig - unter anderem auch - von der Geschwindigkeit“ die einzig korrekte Darstellung eines - objektiven - Zusammenhanges.

Diese Formulierung wäre richtig, wenn wir einmal von der Schwierigkeit absehen könnten, die Geschwindigkeit definieren zu müssen. Mit Gesichtspunkten dieser Problematik setzten wir uns bereits auseinander.

Die herkömmliche Deutung erscheint als nichts anderes als das Resultat einer überaus gedankenlosen Handhabung eines der vormals grundlegendsten Begriffe der Mechanik: den der Masse.

Wir sehen also am Beispiel der Analyse des Massebegriffes, dass hier einige Probleme auftreten können, die schwerwiegende Folgen nach sich ziehen, macht man sich keine Gedanken darüber, wie bestimmte Begriffe historisch entstanden und wie die damit verbundenen Quantitäten wirklich ermittelbar sind. Die Grundhaltung, um die es uns geht, ist doch die, dass man mit Recht fordern sollte, dass die der Physik zugrundeliegenden Begriffe durchaus einer strengen Definition bedürfen. Und in der Physik heißt „strenge Definition“ nun einmal nichts anderes als die Angabe einer - wenigstens prinzipiell denkbaren Messvorschrift. Eine solche Vorschrift aber im Falle der Masse ist, da können wir anstellen was wir wollen, (noch?) nicht gegeben.

Für Ernst Mach war der ursprüngliche Massebegriff als „Materiemenge“ ohnehin nicht sinnvoll, weil prinzipiell nicht messbar, da auch er von der dynamischen Bestimmung der Masse (also Trägheit) - als einzig mögliche beobachtbare Größe - ausging, allerdings ohne der Bedeutung der Gleichwertigkeit von träger und schwerer Masse wirklich konsequent auf den Grund zu gehen, was Einstein später vollzog. Weil aber Ende des 19. Jahrhunderts solche Überlegungen noch nicht relevant waren, beeinflussten sie den weiteren Verlauf der physikalischen Forschung nicht unmittelbar. Und als die wahre Bedeutung dieser Gedanken sich hätte erweisen können, war die Physik längst andere Wege gegangen (z.B. Spezielle Relativitätstheorie), ohne sich mit den grundsätzlichen Dingen - auch im Sinne Ernst Machs - auseinanderzusetzen. Die Weichen waren gestellt. Wenngleich Mach, Einstein und die Allgemeine Relativitätstheorie immer gern in einen Zusammenhang gebracht werden, möchte ich eindeutig darauf hinweisen, dass Einstein s Gedanken keine logische Folge der Ansichten Machs waren. Beide Wege waren verschiedene Wege! Von Mach lernte Einstein , sich mit bestimmten Fragen auseinanderzusetzen; die Antworten Einsteins bewegten sich auf einer ganz und gar anderen Ebene des Denkens (Einstein hielt, im Gegensatz zu Mach, an der Realität des Raumes fest. Für Mach hingegen war der Raum Ausdruck der räumlichen Beziehungen der materiellen Objekte untereinander; und ohne jene Objekte wäre er, wie er es im Zusammenhang mit der Zeit ausdrückte , „ein müßiger metaphysischer Begriff“.), zumal Mach selbst „lediglich“ den analytischen Teil (hier der Mechanik) abhandelte. Mit der konstruktiven Seite befasste Mach sich nicht mehr, womit vielleicht erklärlich ist, dass er zwar Einsteins Theorien anfangs abwartend bis wohlwollend gegenüberstand, wissend, dass diese nicht seiner eigenen Denkrichtung entsprachen, keineswegs jedoch feindselig, da seinerseits mit keiner konkreten Alternative verknüpft. (Hier spielen noch andere Überlegungen bei Mach eine Rolle, auf die einzugehen ich im Rahmen meiner Darlegungen verzichte.)

Nur aus der historisch entstandenen Massebestimmung im Zusammenhang mit der Trägheit (Newton) erfolgte anscheinend so etwas ähnliches wie eine indirekte Messvorschrift, die aber bei etwas näherer Betrachtung sich als eine unzulässige Vermischung grundverschiedener Dinge herausstellt, wobei dieser Fehler jedoch zur damaligen Zeit keine Rolle spielte, weil aufgrund der experimentellen Befunde im Rahmen des damals gegebenen Erfahrungshorizontes die Abhängigkeit der Trägheit nur von der Masse recht naheliegend schien. Die Vermischung zweier völlig verschiedener Dinge aber wurde - trotz neuer Erkenntnisse - bis heute beibehalten!

Alte Anschauungen bedingen neue Ansichten. Kommen wir deshalb wieder auf das Beispiel der Gegenüberstellung der Gewichte von Deuterium und Helium zurück, so erfährt der sogenannte Massendefekt eine Deutung, die aus der Gleichsetzung von Masse und Trägheit (bzw. Gewicht) folgt: Die fehlende Masse ist die Energie, die bei Kernverschmelzung auftritt. Und diese Energie ist eine gewaltige! Sie lässt sich auch rechnerisch mit einer einfachen Formel bestimmen. Diese Gleichung ist die bekannteste und berühmteste und konsequenzenreichste Formel, Synonym gleichsam für bahnbrechende Forschungsergebnisse und Genialität (Einstein), der Physik überhaupt. Und hier lasse ich es mir nicht nehmen, doch eine Gleichung in den Text aufzunehmen, zumal sie fast jeder kennt, wenngleich deren Interpretation weniger geläufig sein dürfte:

E = m· c²

Konkretes Rechenbeispiel: Ein „Massen“-Defekt bei kernphysikalischen Reaktionen (nur dort ist er groß genug, um nachweisbar zu sein) von einem Gramm entspricht einer Energie von 8,99×10¹³ Joule (Wattsekunden) oder ca. 25.000 Megawattstunden. Dies auch ist die Energie, die man benötigen würde, um ein Gramm Masse auf etwa 87% der Lichtgeschwindigkeit zu beschleunigen, denn bei ungefähr dem 0,866-fachen der Geschwindigkeit des Lichtes hätte eine Masse sich verdoppelt.

Karl Popper Ich bin begeisterter Anhänger der Wissenschaft. Physik und Biologie sind für mich großartige Wissenschaften, und ich halte die meisten Physiker und Biologen für sehr gescheit und gewissenhaft. Aber: Sie stehen unter Druck. Diesen Druck gibt es erst seit dem Zweiten Weltkrieg, seitdem so viel Geld für die Wissenschaft ausgegeben wird. Wer eine vorherrschende Mode angreift ist „draußen“ und erhält - vielleicht - kein Geld mehr. Das ist alles sehr traurig. Ja, die Wissenschaft ist leider gefährdet - ihre ursprüngliche Reinheit ist, leider, nicht mehr selbstverständlich.

In Wahrheit jedoch müssten wir korrekterweise formulieren: Bei 87% der Lichtgeschwindigkeit setzt eine gegebene Masse ihrer weiteren Beschleunigung einen Trägheitswiderstand entgegen, der sich gegenüber dem Zustand der Ruhe verdoppelt hat. Oder kürzer: Die Trägheit hat sich unter den genannten Umständen bei gegebener Masse verdoppelt. Dies ist eine völlig andere Aussage (!!!), und doch ändert dieser Umstand nichts an der Tatsache, dass ein mit etwa 259.000 Kilometer pro Sekunde in die Erdatmosphäre eintauchender und nur ein Kilogramm Masse besitzender Meteor bis zur seiner vollständigen Abbremsung (in der Atmosphäre und beim Aufprall) eine Energie von 25.000.000 Megawattstunden umsetzt. Gott sei Dank haben solche kosmischen Geschosse nie die Erde erreicht.

Oder...?

Jedenfalls würden solche Meteore eine ungeheure Verwüstung anrichten, dabei aber im Nachhinein nicht mehr körperlich nachweisbar sein.

Die Energie also besitzt, da mit Masse behaftet, materiellen Charakter - weil dies stillschweigend bei der klassischen Massebestimmung, die sich korrekterweise jedoch nur auf die Trägheit (dynamische Eigenschaft) beziehen dürfte, vorausgesetzt wurde. Da auch elektromagnetische Vorgänge mit Energietransfer verbunden sind, versteht es sich von selbst, dass elektromagnetische Wellen auch Masse besitzen.

Wir werden uns noch damit auseinanderzusetzen haben, dass „elektromagnetische Wellen“ doch mit einer Masseübertragung einhergehen, aber nicht im Sinne der formalen Äquivalenz von Masse (Trägheit) und Energie, sondern in Form von „Teilchen“, den trägheits- aber nicht masselosen Photonen, als „Quanten des elektromagnetischen Feldes“. Die „real existierenden“ Felder werden wir damit jedoch nicht retten. Das Gegenteil ist der Fall.

Folgende interessante Überlegungen könnten die zur Materie gewordene Energie ergänzen. Nehmen wir unseren Bleiwürfel, dessen Temperatur wir jetzt um - sagen wir - 100 Grad erhöhen. Anschließend bestimmen wir das Gewicht jenes Körpers und konstatieren eine Gewichtszunahme, die sich durch die zugeführte Wärmeenergie entsprechend der Einsteinschen Formel erklären lässt.

Selbstverständlich stellen wir nichts fest, da der Effekt zwar grundsätzlich vorhanden ist aber durch eine läppische Energiezufuhr infolge einer Temperaturerhöhung um 100 Grad so gering bleibt, dass selbst utopische Präzisionstechnik ihn unter keinen Umständen direkt messbar werden ließe . Zum Glück ist dieser Effekt derart gering, dass man ihn unmittelbar nicht messen kann. Denn wäre er mit traditionellen Mitteln beobachtbar, so hätte dieser Umstand noch Anfang vergangenen Jahrhunderts recht eigenartige Beweiskraft gehabt. Es galt einst die Auffassung, dass Wärme an das Vorhandensein eines Wärmestoffes gebunden war. Somit hätten wir mit der Wägemethode den „absolut unwiderlegbaren Beweis“ in der Hand gehabt - für die Existenz dieses Stoffes! Um wieviel schwerer hätte es dann die dynamische Sichtweise (statistische Mechanik) des Phänomens Wärme gehabt (wenn überhaupt), sich durchsetzen zu können!

Natürlich käme kein Physiker auf die groteske Idee, im Nachhinein den Wärmestoff aus der Mottenkiste verstaubter Theorien hervorzukramen und zu neuem Glanze zu verhelfen. Wir wissen es halt besser. Und das stimmt vielleicht wirklich. Doch leider nur zum Teil. Die „Masse“-Änderung infolge von Energieänderung ist im Falle der Veränderung des Bewegungszustandes - des makroskopischen Körpers als Ganzes oder als Bewegung der Bestandteile eines Körpers in Form der thermischen Bewegung beispielsweise - in Wahrheit eine Änderung der Trägheit. Das wissen wir jetzt. Aber Energie ist nur in besonderen Fällen Bewegung(senergie). Noch einmal: Führen wir einem Körper Bewegung zu, indem wir ihn beschleunigen (geordnete mechanische Bewegung) oder ihm Wärme zuführen (ungeordnete Bewegung), so verändert sich sein dynamisches Verhalten bezogen auf das Mach sche Bezugssystem dahingehend, dass sein Trägheitswiderstand zunimmt.

Der „Massen“-Defekt bei kernphysikalischen Prozessen hat - im Verständnis der etablierten Physik - nicht das geringste zu schaffen mit Bewegung. Auch die „chemische Bindungsenergie“ ist damit vergleichbar. Beide Energieformen lassen sich unter bestimmten Bedingungen umsetzen in verschiedene Formen der Bewegungsenergie; sie selbst aber sind keine dieser Formen. Warum jedoch nicht?

Vom Wärme-Stoff konnte man sich trennen. Doch wird jetzt aus jeder Form der Energie Materie. Damit haben wir den Wärmestoff, auf höherer Ebene zwar und in verallgemeinerter Form, doch noch rehabilitiert. Ist aber nicht jede Form der Energie konsequenterweise eine Erscheinungsform der Bewegung? Folgendes aufschlussreiche Zitat fügt sich fast nahtlos in unsere Überlegungen ein (C. F. v. Weizsäcker, Zum Weltbild der Physik (Die Auswirkungen des Satzes von der Erhaltung der Energie in der Physik), Stuttgart 1990, S 57 f.):

Carl Friedrich v. Weizsäcker Die materielle Wärmetheorie hielt die Wärme für eine Art Materie, welche weder entstehen noch vergehen könne. Schon die Beobachtung der unbegrenzten Wärmeproduktion durch Reibung widersprach dieser Annahme, und mit der Anerkennung der Wärme als einer Energieform unter anderen war der Bruch mit der alten Theorie vollzogen. Die neue Lehre nannte man im allgemeinen die „mechanische Wärmetheorie“. Damit war zunächst noch nicht die Ansicht bezeichnet, dass Wärme in Wirklichkeit eine Form der Bewegung sei, sondern nur, dass sie in mechanische Arbeit übergeführt werden könne. Mayer selbst fasste die Wärme nicht als Bewegung, sondern als eine selbständige Energieform auf. Er sagte, so wenig man aus der Überführbarkeit der potentiellen Energie in Bewegung folgere, die potentielle Energie sei in Wirklichkeit Bewegung , ebensowenig könne man aus der Überführbarkeit der Wärme in Bewegung folgern, die Wärme sei selbst eine Art der Bewegung. Konsequenterweise müssten wir aber zu genau diesem Schluss gelangen. Am Beispiel des Gravitationsfeldes kamen wir bereits überein, dass hier eine Form der „versteckten Bewegung“ vorliegen könnte. Diese Annahme wird durch die Gleichwertigkeit von Trägheit und Gravitation weitgehend gestützt, wenn nicht gar gefordert. Dieses Thema behandelte ich schon mehrmals recht ausführlich. Sind wir allerdings noch konsequenter, so müssten wir überall dort, wo im traditionellen Sinne von „potentieller Energie“ die Rede ist, ebenfalls eine „verborgene Dynamik“ vermuten. Allerdings haben wir uns dann von der Newtonschen Vorgabe ein für allemal trennen. Und von allen Folgerungen, die historisch und logisch davon abhängig sind - und es gibt keine Aussage der Physik, die nicht davon abhängt -, natürlich auch. Trotzdem hat gerade der Energiesatz am meisten zur Ausbreitung derjenigen „mechanischen Naturauffassung“ beigetragen, die der Meinung war, alle Phänomene der beobachtbaren Natur würden durch rein mechanische Wirkungen der kleinsten Teile der Materie (und des hypothetischen Äthers) hervorgebracht; ja eine physikalische Theorie stelle noch keine wirkliche Erklärung der von ihr behandelten Erscheinungen dar, solange sie diese Erscheinungen nicht auf Mechanik zurückgeführt habe. Durch diese Ansicht wird nämlich der allgemeine Energiesatz als besonderes Naturgesetz entbehrlich. Denn wenn man annimmt, dass alle zwischen den kleinsten Teilchen auftretenden Kräfte Diese Formulierung lässt die Inkonsequenz auch bei C. F. v. Weizsäcker erkennen. Wenn wir alle Physik auf Mechanik zurückführen wollten, so müssten wir uns von der Newtonschen Mechanik trennen und von den „verursachenden Kräften“ ebenso. durch eine nur von ihrer gegenseitigen Lage abhängigen Energie Diese „von ihrer gegenseitigen Lage“ abhängige Energie ist eben die potentielle Energie, die, sind wir wirklich konsequent, ihrerseits auf Dynamik zurückgeführt werden müsste. bestimmt sind (dass es also im kleinen keine Reibung gibt), so gilt vermittels der mechanischen Grundgesetze automatisch der Energiesatz. Die empirisch allgemeine Gültigkeit des Energiesatzes ist dann nur ein Hinweis auf die Geltung dieser verborgenen Mechanik und eine Aufforderung, die in der Erfahrung auftretenden Energiearten auf mechanische Energieformen der kleinsten Teilchen zurückzuführen. So gilt dann z.B. die Wärme als kinetische Energie, die chemische Energie als eine bestimmte potentielle Energie der Atome. Man hat nach Helmholtz diesen Gedankengang geradezu als Begründung des Energiesatzes verwendet. Eine Fülle von Erfahrungen hat schließlich in der Tat bewiesen, dass Wärme als ungeordnete Bewegung der Atome aufgefasst werden muss. Die auf dem Energiesatz basierende Thermodynamik ist dadurch auf eine statistische Mechanik gegründet worden. Um so wichtiger ist daher vom grundsätzlichen Standpunkt aus, dass der Energiesatz auch in der Elektrodynamik gilt, welche nicht hat auf Mechanik zurückgeführt werden können Tatsache ist: auf die Newtonsche Mechanik lässt sie sich nicht zurückführen, weil Wesensmerkmal dieser Mechanik die Trennung von Kinematik und Dynamik ist. dass die „mechanische Wärmetheorie“ überhaupt erfolgreich sein konnte liegt in der Tatsache begründet, dass sie von den konkreten Wechselwirkungen der „kleinsten Teilchen“ absieht, und das „Billardkugel-Modell“ (nur die lineare Bewegung und der elastische Stoß sind relevant) in diesem Zusammenhang mit hinreichender Genauigkeit der Realität sehr nahe kommt.

Fassen wir zusammen:

1. Der überaus wichtige Massebegriff ist in der Mechanik überhaupt nicht definiert.
2. „Masse“ wird einerseits als Synonym für „Trägheit“ (eine Eigenschaft) genommen, aber andererseits wird der Massebegriff noch immer mit „Materiemenge“ in Verbindung gebracht.
3. Korrekterweise darf der Massebegriff nur im Sinne von „Trägheit“ verwendet werden.
4. Die Trägheit ist eine dynamische Größe, die nur im Machschen Sinne (Machsches Prinzip) einigermaßen - zumindest qualitativ - erklärbar ist.
5. Aufgrund der quantitativen Gleichheit von Trägheit und Gravitation sowie der Annahme, dass diese auf einer qualitativen Idendität beruht, kann die Gravitation auch nur als dynamische Erscheinung der Wechselwirkung aller Objekte mit dem kosmischen Umfeld gedeutet werden (auch dann, wenn wir noch nicht in der Lage sind, dieser Aussage eine quantitative Gestalt zu geben).
6. Da die Trägheit zudem vom „inneren Energiegehalt“ eines Körpers abhängt („Massen“-Defekt bei kernphysikalischen Reaktionen beispielsweise), folgt logisch zwingend, dass Trägheit nur als Ausdruck einer komplexen Wechselwirkung der „inneren Dynamik“ der Materie mit der „äußeren Dynamik“ des Machschen Bezugssystems angesehen werden darf. Auch in der Schulphysik geht man davon aus, dass die „Bausteine der Materie“ sich in steter Bewegung befinden, wobei dieser Bewegungsbegriff nicht mit dem „einfachen“ mechanischen Bewegungsbegriff verglichen werden darf.

Wichtig:

Die größte Fehleinschätzung aller Zeiten der Physiker besteht meiner Überzeugung nach darin, den klassischen mechanischen Bewegungsbegriff als „einfach“ einzustufen! Diese Bewegung ist, wie wohl die bisherigen Darlegungen nahelegen, alles andere als einfach; und ich konnte nachweisen, dass dieser „einfache“ mechanische Bewegungsbegriff bis in die heutigen Tage nicht sinnvoll und widerspruchsfrei und allgemeingültig erklärt ist.

Alle bisherigen Fehleinschätzungen beruhen auf dem Vorurteil, dass die materiellen Strukturen auf den verschiedenen hierarchischen Strukturebenen (eine Auswahl: Galaxien, Planetensysteme, Atome, Elementarteilchen) voneinander unabhängig sind. Wie ich an dieser Stelle ohne Beweis mitteile, sind sie lediglich „relativ unabhängig“, aber es gibt Systemeigenschaften (eine sehr wichtige Eigenschaft ist die Trägheit, im üblichen Sprachgebrauch die Masse), die möglicherweise ausschließlich hierarchieübergreifend erklärt ist. Alle empirisch verifizierten Erkenntnisse (z.B. die energieabhängige Trägheit als Massezunahme gedeutet) werden in das vorhandene Gedankensystem integriert, ohne zu beachten, dass dieses System historisch gewachsen ist, wobei naturgemäß auf künftige empirische Befunde nicht vorgegriffen werden konnte. Wären Galilei und Newton auch nur einige wenige Erfahrungstatsachen aus den Gebieten der Atom- und Teilchenphysik bekannt gewesen, die Entwicklung der Physik hätte mit hoher Wahrscheinlichkeit einen gänzlich anderen Verlauf genommen!

Alles, was sich bei den Ausführungen dieses Kapitels auf den Massebegriff bezog, lässt sich auch auf andere Dinge verallgemeinern. Wichtigste Erkenntnis: Es ist nicht immer möglich, Eigenschaften der Materie (hier die Trägheit) aus dem „kosmischen Zusammenhang“ losgelöst zu betrachten. Sicherlich gibt es „hierarchieeigene“ Beziehungen, die ohne hierarchieübergreifende und damit komplexe Zusammenhänge auskommen. Aber es ist nie von vornherein entscheidbar, welcher Fall gerade vorliegt. Für eine solche Entscheidung wären Kenntnisse erforderlich, die möglicherweise dem tatsächlich gegebenen historischen Verlauf der Physikentwicklung vorauseilen, zu denen man doch erst gelangen will. Und diese notwendigen Erkenntnisse bleiben in unerreichbarer Ferne, weil alle Erscheinungen auf Grundlage des gegebenen Wissensstandes interpretiert werden. Und diese Interpretation kann grundsätzlich falsch sein, wie es die Analyse des Massebegriffes zeigt.

Dazu einige grundlegende Bemerkungen, die sich nicht nur auf den Massebegriff beziehen. Die Physiker sind einigermaßen stolz auf ihre Errungenschaften. Und als eine wesentliche Errungenschaften der Physik gilt deren Vorgehensweise: die traditionelle wissenschaftliche Methode. Dazu hatte ich bereits Stellung bezogen. Mathematisierte Theorie auf der einen Seite sowie Beobachtung und Experiment auf der anderen. Dies allein wird akzeptiert. Es läuft darauf hinaus, Aussagen der Form

A gleich B

zu gewinnen. Und im Experiment oder der Beobachtung wird dann überprüft, ob diese Aussage wahr ist oder auch nicht. Erweist sich diese Aussage eindeutig als falsch (Mess- und Beobachtungsfehler sowie Manipulationen ausgeschlossen), so stimmt mit der Theorie etwas nicht (Falsifikation). Im Falle eines positiven Befundes (Verifikation) hat man zwar noch keinen endgültigen Beweis für die Richtigkeit der Theorie in der Hand (es kann immer noch vorkommen, dass unter anderen Bedingungen diese Hypothese sich als falsch erweist), aber es besteht die berechtigte Hoffnung, der Wahrheit ein Stück näher gekommen zu sein. Dabei setze ich voraus, dass die Aussage „A gleich B“ wirklich eine - zunächst hypothetische - Gesetzmäßigkeit abbildet. Mit einer solchen Hypothese hatten wir uns im obigen Text und einem der vorausgegangenen Kapitel eingehend beschäftigt:

träge Masse gleich schwere Masse.

Mit einer sehr hohen Genauigkeit konnte diese Hypothese bisher bestätigt werden. Allerdings gibt es dabei, sollte diese Aussage eine objektive Aussage sein, ein schwerwiegendes Problem: Die beiden Massebegriffe müssten unabhängig von dieser Aussage und unabhängig voneinander definiert sein. In diesem Kapitel konnte nachgewiesen werden, dass der Massebegriff im üblichen Sinne (Materiemenge) überhaupt nicht definiert ist. Es wäre nämlich notwendig, streng zwischen „Masse“ und „Trägheit“ zu unterscheiden. Und die „Schwere“ ist nach unserer jetzigen Kenntnis auch nur Ausdruck der Trägheit. Auch das 2. Newtonsche Axiom hilft uns nicht weiter:

Die Beschleunigung ist gleich Kraft dividiert durch Masse.

Sollte diese Beziehung eine objektive (empirisch kritisierbare) Gesetzmäßigkeit abbilden, so wäre zu fordern, dass alle in dieser Relation vorhandenen Größen unabhängig voneinander definiert sein müssten. Wie wir bereits erkennen konnten, ist dies für die Beschleunigung (die sich immerhin auf ein Inertialsystem beziehen muss; die Zeit kommt später dran) sowie die Masse nicht gegeben.

Auch wenn ich noch nicht auf alle Zusammenhänge eingehen konnte (dies würde auch den Rahmen dieses Textes sprengen), so folgt als wichtigste Aussage aller bisherigen Bemühungen (selbst wenn der Leser noch nicht sämtliche logischen Abhängigkeiten schon überblicken kann):

Alle Begriffe der klassischen Mechanik definieren sich gegenseitig. Damit beschreibt nicht eine einzige Aussage dieser Mechanik irgendwelche objektiven Gesetze qualitativ richtig. Aufgrund ganz bestimmter Bedingungen erscheinen die quantitativen Fehler als vernachlässigbar klein. Und die „ganz bestimmten Bedingungen“ beziehen sich auf den raumbezogenen Bewegungsbegriff (raumbezogene Kinematik), der wegen der konkreten „kosmischen Dynamik“ (quasistatisches Bezugssystem in Gestalt der „un“beweglichen kosmischen Objekte) zwar qualitativ falsch ist, jedoch durchaus näherungsweise zu quantitativ richtigen Rechenergebnissen führen kann.

Wenn diese Sätze richtig sein sollten, so folgt zwingend: Die Physik befindet sich in der Sackgasse, und mit ihr auch alle die Physik anwendenden Wissenschaften. Dazu ein Beispiel aus dem nicht gerade leichten Leben der Astronomen und Astrophysiker.

Mit ziemlicher Sicherheit glaubt man zu wissen, auf welche Weise „das Universum“ strukturiert sei und wie es entstanden ist. Ich erwähnte in diesem Text bisher zwei dieser Strukturebenen: das Sonnensystem und die Galaxis (wenn unser Milchstraßensystem gemeint ist bzw. die Galaxien (wenn diese Systeme als Allgemeinbegriff angesprochen werden). Nun tummeln sich die Galaxien nicht irgendwie völlig regellos und chaotisch im All umher, sondern bilden ihrerseits wiederum irgendwelche Strukturen, die „Galaxienhaufen“, welche selbst wieder irgendwelchen „Superhaufen“ und „großen Mauern“ (Die Einzelheiten sind nicht so wichtig, ich kenne mich da auch nicht so genau aus; auf die Tatsache der Strukturbildung in kosmischen Dimensionen überhaupt kommt es an.) angehören sollen. Ein Ende ist nicht abzusehen. All diese Strukturen (gehen wir einmal berechtigterweise davon aus, dass sie existieren) müssen seit dem Urknall (gehen wir einmal unberechtigterweise davon aus, dass er stattfand) sich gebildet haben. Dies führt zu erheblichen Problemen, auf die ich nicht im Detail eingehen möchte. Jedenfalls dürften aus verschiedensten Gründen diese Strukturen noch nicht oder überhaupt nicht sich gebildet haben können.

Doch ganz so weit brauchen wir uns gar nicht hinauszubegeben, denn schon die konkrete Dynamik der Galaxien widerspricht offensichtlich den Gesetzen der Mechanik. Deren Rotation (relativ zum „extragalaktischen Hintergrund“?) dürfte nicht in dieser Weise stattfinden, wie sie nun einmal stattfindet. An unseren Vorstellungen gemessen, rotieren sie recht langsam, aber hierbei würden die auftretenden Fliehkräfte weitaus größer sein als zulässig. Die Galaxien müssten „auseinanderfliegen“. Und hier besann man sich der Verfahrensweise, die bereits im vergangen Jahrhundert erfolgreich war: Die Abweichungen einer beobachteten Bewegung von der theoretisch zu erwartenden muss eine Ursache haben, die in irgendwelchen „verborgenen unsichtbaren“ Massen zu finden sein muss. Beim Planeten Neptun ging diese Rechnung aufgrund glücklicher Begleitumstände (und wirklich nur deshalb) fast auf. Warum sollte eine bewährte Denkweise nicht auch bei neuen Problemlösungen sich abermals bewähren?! Nochmals: Aufgrund der bekannten Verteilung der Sterne innerhalb einer Galaxie sowie der ebenfalls bekannten gravitativen Anziehungskräfte müsste sich ein Rotationsverhalten errechnen lassen, das mit der beobachtbaren Kinematik - innerhalb der Fehlergrenzen - in Übereinstimmung zu bringen sein müsste. Dem aber ist nicht so. Es treten eklatante Divergenzen auf, die sich dann nur beherrschen lassen, führt man - neben der bereits beobachteten Materie - weitere Massen ein, die durch ihre Gravitationswirkung wieder Ordnung in das Geschehen zu bringen in der Lage sind und für die Stabilität der Sternsysteme sorgen. Das Problem: Die „unbeobachtbare Materie“ müsste 90% der Gesamtmasse der Galaxie ausmachen! Die Gesamtmasse der Galaxien wäre damit 10mal größer, als es herkömmliche astronomische Beobachtungen bislang nahezulegen schienen!

Also wurde die Hypothese von der „Dunklen Materie“ geboren. „Dunkel“ heißt hier nicht einfach nur, dass diese Materie (noch) zu kalt sei, um selbst Licht oder sonstige elektromagnetische Strahlung auszusenden, sondern, dass sie mit der „normalen Materie“ nur und ausschließlich über die Gravitation in Wechselwirkung tritt, sonst nicht. Interstellare und intergalaktische Gas- und Staubmassen zählen vielleicht dazu; die aber sind nicht „dunkel“, sondern nur „kalt“. Mögliche Kandidaten z. B. sind „Schwarze Löcher“ und „Neutronensterne“ und andere Exoten. Und die Neutrinos waren lange Zeit im Gespräch. Auch über noch völlig unbekannte Materiearten denkt man bereits sehr laut nach.

Zwei Probleme hat man sich damit eingehandelt: Erstens musste man sich darum kümmern, diese Dunkelmaterie unabhängig von den Beziehungen nachzuweisen, zu deren Zweck sie eingeführt wurde; und zweitens stellt diese exotische Materie, wie schon angedeutet, nicht irgendeine nebensächliche Randerscheinung dar, die einen bestimmten nebensächlichen Effekt erklären soll, der ohne sie nur ungenau begründbar wäre, sondern sie wäre wesentlicher Bestandteil der Galaxien überhaupt. Dieses Problem deutet darauf hin, dass die „gewöhnliche Materie“ der Galaxien (Sterne, Gas- und Staubmassen) beispielsweise nur bescheidene 10% deren Gesamtmasse ausmachen soll! Hier handelt es sich nicht um eine - lediglich die Genauigkeit steigernde - Korrektur, sondern um ein existenzielles Problem!

Hier möchte ich mich nicht in Einzelheiten verlieren. Welcher Art von unsichtbarer Materie man auch gern haben möchte, alles hängt mit der „Masse“ zusammen und deren „Gravitationswirkung“ und der „Trägheit“. Wie auch immer mögliche Schlussfolgerungen ausfallen mögen, von einer physikalischen Größe - der Masse eben - werden alle Folgerungen abhängen! Ausnahmslos alle - jetzigen und künftigen - Überlegungen sind geprägt von diesem historisch entstandenen und überhaupt nicht sauber definierten Begriff!

Sind unsere bisherigen Überlegungen in diesem Text - insbesondere die in diesem Kapitel - nicht gänzlich unsinnig, so bemerkt man die Sinnlosigkeit der Bemühungen der Physiker um die Deutung der konkreten Struktur des Universums. Bevor man nach irgendwelcher exotischen Materie Ausschau hält und die verwegensten theoretischen Konzepte entwirft, wäre es doch viel naheliegender, über all die diesen Überlegungen zugrundeliegenden Begriffe und Basisvorstellungen einige Überlegungen anzustellen! (Hierzu einige weitere Überlegungen im Text “Gottes Urknall”)

Verstehen wir die Masse als eine Eigenschaft der Materie, nämlich die der Trägheit, so kehrt sich die ganze Schlussweise um. Die Trägheit  und mit ihr die Gravitation - ist eine dynamische Größe, die sich aus den konkreten (hier wahrscheinlich galaktischen?) Bewegungsverhältnissen ergibt. Wie auch immer wir „Bewegung“ konkret verstehen wollen, so ist nicht die „Masse“ die Ursache für diese Bewegungsverhältnisse; sondern umgekehrt ergibt sich die Masse (verwenden wir „Masse“ für „Trägheit“ und „Schwere“) als Resultat dieser Dynamik. Damit hat sich die Fragestellung aber umgekehrt, ungeachtet der Tatsache, dass wir diese Frage - die Frage nach der Dynamik - noch nicht beantworten können. Zumindest erübrigt es sich dann, nach irgendwelcher Dunkelmaterie zu fahnden.

Immer dann, wenn wir bestimmte Zusammenhänge nicht verstehen, werden „verborgene Ursachen“ vermutet, die einstmals sich als Geister, Götter und Dämonen manifestierten. Dieses Thema möchte ich nicht nochmals aufwärmen, zumal uns die Naturwissenschaften ein großes Stück rationaler Welterkenntnis bescheren konnten. Allerdings gibt es auch hier einige „Geisterstoffe“, von denen ich drei bereits nennen konnte. So hatte man erst in diesem Jahrhundert endgültig Abschied genommen von dem alles durchdringenden „Äther“. Er passte spätestens seit der Speziellen Relativitätstheorie nicht mehr ins physikalische Bild. Und der „Wärmestoff“ seligen Angedenkens musste der statistischen Mechanik weichen. Dann tauchten die „Felder“ auf, zu denen man ebenfalls nur indirekt - über deren „Wirkungen“ - sich Zugang verschaffen konnte. Die Felder sind die Vermittler der Wechselwirkungen. Einige dieser Zusammenhänge konnten wir bereits analysieren. Letztlich verdanken die Felder ihre „Existenz“ der noch immer gültigen Anschauung von Raum, Zeit, Bewegung und Wechselwirkung.

Bei Ernst Mach konnten wir bereits nachlesen (E. Mach, Die Mechanik in ihrer Entwicklung, Leipzig 1933, Nachdruck: Darmstadt 1991, S. 227 f.):

Ernst Mach Wenngleich auch ich erwarte, dass astronomische Beobachtungen zunächst nur sehr unscheinbare Korrektionen notwendig machen werden, so halte ich es doch für möglich, dass der Trägheitssatz in seiner einfachen Newtonschen Form für uns Menschen nur örtliche und zeitliche Bedeutung hat.

Hier hatte Mach zweifelsohne recht. Nur in einem Punkt irrte er gewaltig: Er sprach von „unscheinbaren Korrektionen“. Unscheinbar sind die Korrekturen, die notwendig sein könnten, mitnichten. Schon die Dynamik der Galaxien ist innerhalb der geläufigen Denkschemata nicht sehr verständlich. Und die „unscheinbare Korrektion“ erfordert die Annahme einer „dunklen Materie“, die angeblich 90% der Gesamtmasse der Milchstraßensysteme ausmachen soll! Weiter oben deutete ich das Problem des „Massendefektes“ im atomaren Bereich an. Hier zeigte es sich, dass die Eigenschaft der Trägheit keine statische additive Größe ist. Wegen der Vermischung von „Masse“ und „Trägheit“ sprechen die Physiker noch immer vom „Massendefekt“, der als vergegenständlichte Energie gedeutet wird. Nichts anderes finden wir möglicherweise bei der Dynamik der Galaxien. Hier allerdings beträgt der „Massendefekt“ stattliche 90%, wobei man diese Differenz wirklich als (noch) nicht beobachtbare „echte“ Materie deutet.

Nochmals: Die Indizien deuten darauf hin, dass die Gesamtmasse der Galaxien nicht einfach durch die Summe der Einzelmassen der Sterne gebildet wird, sehen wir hierbei einmal von dem durchaus abschätzbaren Anteil „kalter Materie“ (interstellare Gas- und Staubmassen) ab. Die „Gesamtmasse“ muss scheinbar größer sein, als sie es der Anzahl der Sterne nach sein dürfte. Da aber die Masse nur als Trägheit verstanden werden kann, ergibt sich auch die Einzelmasse (sprich: Trägheit) eines Sternes aus der konkreten Dynamik der übergeordneten Struktureinheit (Galaxie), deren Bestandteil er ist. Damit aber ist so etwas wie eine Gesamtmasse (als Trägheit verstanden) für ein ganzes Milchstraßensystem überhaupt nicht im traditionellen Sinne definiert. Hier spielen - vermutlich - andere Beziehungen eine Rolle, von denen wir noch weniger verstehen! Hier gelangen wir in der Systemhierarchie einen Schritt in Richtung Galaxienhaufen usw., wobei auch hier in der Astronomie und Astrophysik von abschätzbaren „Gesamtmassen“ die Rede ist. Je weiter wir uns in die „überstellaren“ und „übergalaktischen“ Bereiche begeben, um so sinnloser aber werden unsere altbekannten Begriffe!

Und wenn sogar - ein endliches Universum vorausgesetzt, wie auch immer man sich das vorstellen möge - die „Gesamtmasse der Welt“ ermittelt wird, so erinnert eine solche „exakte Berechnung“ - die Einstein -Jünger mögen verzeihen - seltsam an die „korrekte“ Bestimmung der Anzahl der Engel, die auf einer Nadelspitze Platz finden. Newton löste auch dieses Problem, wobei solche - für uns heutzutage abwegig erscheinenden Betrachtungen - die tatsächliche Leistung eines Isaac Newton nicht herabwürdigen.

An dieser Stelle könnte ich dieser Text bereits beenden. Wenn ich nämlich nachweisen kann, dass auch nur ein Begriff im Gesamtgefüge der Physik ein recht fragwürdiges Dasein fristet, so gilt dies für sämtliche Begriffe, Hypothesen und Theorien, die von diesem einen Begriff in irgendeiner Weise abhängig sind. Und Tatsache ist: Es gibt keinen Bereich der Physik, in welchem die fundamentale Größe „Masse“ keine Rolle spielt. Wenn es aber diese fundamentale Bestimmung überhaupt nicht gibt, jedenfalls nicht in der üblichen Verwendung, was dann?!

Zumindest zeigt bereits die Analyse des Massebegriffes, dass erstens „die Welt“ nicht so einfach ist, wie man es immer noch wahrhaben will; und dass zweitens der Erkenntnisstand der Physik nicht einfach nur objektiv reale Verhältnisse widerspiegelt, sondern auch in irgendeiner Weise Abbild des historischen Erkenntnisprozesses ist, wobei ich mich an dieser Stelle auf allzu langweilige Einzelheiten nicht einlassen mag. Diese Einsicht aber ist nicht wirklich neu. Neu vielleicht sind die hier angedeuteten Konsequenzen.

Erkenntniskritische Überlegungen hatten bislang keinerlei Einfluss auf den Prozess der Forschung selbst. Und die Konsequenz des Ernstnehmens solchermaßen kritischer Hinweise wäre es, den gesamten Erkenntnisprozess wirklich unvoreingenommen zu überdenken, aber auch die historisch entstandenen Institutionen der Wissensvermittlung und die der Wissensgewinnung ebenso. Eine solche Kritik allerdings ist indiskutabel, da sie die Tätigkeit derer berührt, welche die Forschung und Lehre betreiben.

Im einem der nächsten Kapitel gehe ich auf ein spezielles Forschungsgebiet die Hochenergiephysik - in groben Umrissen ein. Dabei zeigt es sich, dass Forschung zu einem gewaltigen Wirtschaftsfaktor geworden ist. Und das ist gefährlich. Nicht für die Forscher, sondern für die Wahrheit. Diese Formulierung ist natürlich auch nicht völlig korrekt. Für die Wahrheit kann es gar nicht gefährlich werden, da man ihr ohnehin nicht zu nahe kommen wird. Bei Karl Popper z. B. (Sir Karl Raimund, 1902-1994) finden wir eine interessante Aussage, die ich unkommentiert wiedergeben möchte (Aus einem Interview mit der Zeitung „Die Welt“ im Jahr 1990.):

[Home] [Seitenanfang]