Wie zufällig ist der Zufall? - Prognostizier- und Reproduzierbarkeit
Fünf Dinge gehören zur Prognostizierbarkeit (von Prozessen und Ereignissen):
- Der Objektprozess selbst, über den wir Aussagen machen wollen.
- Das Modell, anhand dessen wir Aussagen über den Objektprozess gewinnen wollen. Wird das Modell selbst als Prozess realisiert, so sprechen wir vom Modellprozess oder einer
Simulation.
- Quantitative Aussagen über die Anfangsbedingungen und Randbedingungen des Objektprozesses. (Hier berühren wir zum ersten Mal die Problematik des Messprozesses.)
- Vergleich der Objektparameter mit den Modellparametern. Jetzt müssen abermals die Objektparameter bestimmt werden. Im allgmeinen lassen sich aus dem Grad der Übereinstimmung
zwischen Modell und Objekt Aussagen über das Modell gewinnen (Verifikation oder Falsifikation.)
- Und schließlich dürfen wir nicht das Referenzsystem in Gestalt unserer schon mehrfach zitierten Uhr vergessen, welche den notwendigen Referenzprozess (Zeitmaßstab) realisiert.
Jetzt sich mit allen in diese Aufzählung versteckten Problemen zu befassen (es gibt eine ganze Menge davon), würde zu weit führen. Deshalb vereinfachen wir das Ganze und gehen über von der
Prognostizierbarkeit zur Reproduzierbarkeit. Der Unterschied zwischen beiden Dingen erst einmal ist der „Modellprozess“. Dieser wird auf gleicher materieller Substratebene, lediglich zeitversetzt,
realisiert. Ein prognostizierbarer Prozess muss auch reproduzierbar sein. Und umgekehrt. Letzteres wird dann zur reinen Fiktion (Beispiel: astronomische Prozesse), wenn diese Prozesse - von unserem
Standpunkt aus betrachtet - sich unserer Einflussnahme entziehen. (Wir sind eben nicht in der Lage ein „reales astronomisches Planspiel“ zu realisieren - Gott sei Dank.)
Folgende Schlussweise ist somit zulässig: Lassen sich Prozesse reproduzieren, so müssen sie auch determiniert sein. Da klassisch mechanische Prozesse als determiniert angesehen wurden, müssten sie auch
uneingeschränkt reproduzierbar sein. Doch sie sind es nicht. Und weil es zu nichts führt, bleiben wir weiterhin allgemein und abstrakt, nehmen wir - es macht sich wirklich gut - wieder einmal eine
Fiktion zur Hilfe, eine Fiktion, die uns die Voraussetzungen der klassischen Denkweise auf sehr vereinfachte Weise nahebringen soll.
Doch zuvor wollen wir uns noch mit dem Wahrscheinlichkeitsbegriff beschäftigen. (Ganz ohne Mathematik geht es doch nicht, aber nur in sehr bescheidenem Umfang.) Dabei fangen wir mit dem sicher hinlänglich
bekannten Beispiel mit dem Würfel an. Ein solcher Würfel hat sechs Seiten. Damit das „Würfeln“ überhaupt einen Sinn hat, werden die - sonst nicht unterscheidbaren - Seiten gekennzeichnet, indem man
sie durchnumeriert. Wie groß nun ist die Wahrscheinlichkeit, eine „Eins“ zu würfeln? - Also: sechs Möglichkeiten gibt es. Und die „Eins“ ist eine davon. Die Wahrscheinlichkeit, eine solche
„Eins“ zu erwürfeln, beträgt damit 1:6. Dies heißt nicht, bei zwölf Würfen würden wir genau zweimal die „eins“ und zweimal die „Zwei“ usw. erhalten. Aber wiederholen wir den Versuch -
sagen wir - 60.000 mal, so können wir davon ausgehen, die „eins“ ungefähr 10.000 mal zu bekommen.
„Ungefähr“ eben heißt, es könnte folgende Verteilung
(Tabelle 1) auftreten. (Die Zahlen entstammen einer äußerst simplen Computersimulation, da das tatsächliche Würfeln mit einem richtigen Würfel doch etwas langweilig werden würde.) Wie wir sehen, nähert sich die relative Häufigkeit des Eintretens eines bestimmten Zustandes bei großer Anzahl der Versuche der Wahrscheinlichkeit von 1:6 = 0,16666...
Wichtig in unserem Zusammenhang: Die Tabelle zeigt die Verteilung einer diskreten Zufallsvariablen
in einem bestimmten Intervall an. Dies will heißen, die Zufallsvariable kann in unserem Beispiel nur 6 verschiedene Werte annehmen. Und alle diese Werte sind gleichwahrscheinlich. (Wir setzen voraus, dass an dem Würfel keine Manipulationen vorgenommen worden und er aus homogenen Material besteht) Deshalb sprechen wir von einer
gleichverteilten diskreten Zufallsvariablen.
|
Ziffer
|
Absolute Häufigkeit
|
Relative Häufigkeit
|
|
1
|
9924
|
0,1654
|
|
2
|
9899
|
0,1650
|
|
3
|
9971
|
0,1662
|
|
4
|
10039
|
0,1673
|
|
5
|
10012
|
0,1669
|
|
6
|
10155
|
0,1692
|
|
Tabelle 1
Die Wahrscheinlichkeit ist immer ein Wert zwischen 0 und 1. Die „0“ deutet auf den „unmöglichen Zustand“ hin, und die „1“ beschreibt den „mit
Sicherheit eintretenden“. Auf unser Beispiel bezogen heißt dies: die Wahrscheinlichkeit, dass eine der Zahlen von 1 bis 6 gewürfelt wird, beträgt 1, denn eines
der genannten sechs Ereignisse wird mit Sicherheit eintreffen. (Der Würfel wird nicht auf einer Kante oder gar Ecke stehend liegenbleiben.)
Vergrößern wir den Wertevorrat der Zufallsvariablen, so wird die Wahrscheinlichkeit für das Eintreten eines konkreten Ereignisses abnehmen.
Nehmen wir einen Schützen, der aus einer bestimmten Entfernung auf eine Scheibe zielt. Angenommen, diese Zielscheibe weist 10 „Ringe“ auf, so
sind 12 Ereignisse (Tabelle 2) denkbar, 12 deshalb, weil ja durchaus die Scheibe außerhalb des markierten Bereiches getroffen werden kann oder
auch überhaupt nicht. Wieder haben wir eine diskrete Zufallsvariable (mit 12 Werten) aber keine gleichverteilte mehr. Lassen wir uns das an einem
Zahlenbeispiel veranschaulichen, wobei - als Beispiel - 100 Schüsse abgegeben wurden. Die nachstehende Tabelle widerspiegelt kein reales
Ergebnis, sondern die Zahlen sind frei erfunden. Das ist nicht so wichtig. Folgende qualitative Aussage sei dennoch erlaubt: je mehr die genannte
Verteilung von der Gleichverteilung abweicht, um so „besser“ ist der Schütze. Eine der Gleichverteilung nahekommende Verteilung bedeutet: das Schießergebnis wäre vollkommendem
Zufall überlassen (so schlecht kann kein Mensch zielen).
|
Variable
|
Absolute Häufigkeit
|
Relative Häufigkeit
|
|
Zentrum
|
31
|
0,31
|
|
Ring 1
|
20
|
0,20
|
|
Ring 2
|
15
|
0,15
|
|
Ring 3
|
8
|
0,08
|
|
Ring 4
|
7
|
0,07
|
|
Ring 5
|
5
|
0,05
|
|
Ring 6
|
5
|
0,05
|
|
Ring 7
|
4
|
0,04
|
|
Ring 8
|
2
|
0,02
|
|
Ring 9
|
1
|
0,01
|
|
Scheibenrand
|
1
|
0,01
|
|
Nicht getroffen
|
1
|
0,01
|
|
Tabelle 2
Spannen wir schließlich das Gewehr in eine stabile Vorrichtung ein, so dürfen wir davon ausgehen, dass alle Kugeln ins Zentrum treffen. Wir
sprechen immer noch von einer diskreten Zufallsvariablen. Angenommen, wir unterteilten die Zielscheibe nicht in 10 oder 25 „Ringe“, sondern
würden 1.000 Markierungen aufzeichnen; auch dann gäbe es noch eine endliche Anzahl von Möglichkeiten, aber die Wahrscheinlichkeit, eine - und
nur eine - davon zu treffen ist um den Faktor 100 kleiner als zuvor. Wird auch jetzt das fixierte Gewehr in das Zentrum treffen, welches immerhin
100 mal kleiner ist als es das beim ersten Versuch war? - Vielleicht - vielleicht auch nicht. Hier kommen wir jetzt auf die Problematik der
Reproduzierbarkeit zurück. Sind die einzelnen Schüsse aus dem Gewehr wirklich identisch? - Diese Frage muss verneint werden. Immer wird es
nicht beherrschbare Einflüsse geben: Die Pulverladungen und die Geschosse sowie die Patronenhülsen sind nicht völlig gleich, sondern unterliegen
Fertigungstoleranzen. Die Versuchsanordnung ist Temperaturschwankungen unterworfen und was sonst noch als Einwirkungen denkbar sind. Der
Gewehrlauf weist nach jedem Schuss - auch geringfügige irreversible - Veränderungen auf, usw. Gleichgültig wie, die Streuung der Einschüsse wird
sich in Grenzen halten. Aber: wie klein diese Streuung auch sein möge, absolut reproduzierbare Ergebnisse wird es nie geben. Dies hat auch im Rahmen bisheriger Überlegungen keinerlei Bedeutung.
 |
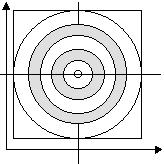Abbildung 1
Versuchen wir jetzt eine quantitative Abschätzung vorzunehmen, indem wir annehmen, der Abstand des Gewehres von der Scheibe betrage 100
Meter, der Durchmesser der Scheibe 1 Meter und der des Geschosses 1 Zentimeter. Dieses Geschoss verlässt den Lauf mit einer Geschwindigkeit
von 500 Meter je Sekunde. Vernachlässigen wir den Luftwiderstand, so benötigt die Kugel 0,2 Sekunden bis zum Auftreffen auf die Scheibe. Wenn
also nichts Unvorhergesehenes passiert, wird das Projektil auch die Scheibe erreichen. Und der Streubereich der Treffer wird nicht allzu groß sein,
und beträgt - um eine optimistische Zahl zu nennen - 1 Zentimeter (unter realen Bedingungen dürfte dieses Ergebnis schwer zu verwirklichen sein.)
Jetzt variieren wir den Versuch dahingehend, dass wir die Bedingungen „geringfügig“ erschweren; und damit es nicht gar zu schwer wird, verlagern
wir den Versuchsaufbau in das All, um einige Störeinflüsse (Luft, Gravitation) auszuschalten. Die Erschwernis besteht zum einen darin, dass wir
größere Entfernungen wählen und wir eine Kausalkette „erzeugen“ wollen. Das hört sich einfach an, aber...
In obiger Skizze (Abbildung 1) sei unsere Zielscheibe dargestellt. Diese befindet sich in einem uns bereits geläufigen (zweidimensionalen)
Koordinatensystem. Jeder Treffer sei durch die Angabe zweier Koordinatenangaben (x und y) spezifiziert. Wie groß dabei ist die Wahrscheinlichkeit
, einen bestimmten Punkt dieses Koordinatensystems zu treffen? - Diese Wahrscheinlichkeit ist gleich Null! Einen Punkt wird man nie treffen. Dieser
Zusammenhang ließe sich nämlich mit einer Wahrscheinlichkeitsfunktion mit zwei stetigen Zufallsvariablen beschreiben. Es lässt sich aber empirisch
ermitteln, in welchem Bereich die Treffer mit höchster Wahrscheinlichkeit zu finden sind. Die Einteilung in solche Bereiche lernten wir in Gestalt der aufgezeichneten Ringe kennen.
Jetzt interessiert uns nicht mehr die konkrete Verteilung, sondern wir wollen nur noch den Bereich angeben, in welchem mit Sicherheit ein Treffer zu
erwarten ist. Zur Veranschaulichung möge folgende Skizze (Abbildung 2) dienen:
Abbildung 2
Weiter oben galten für die angegebenen Parameter folgende Werte: Entfernung E = 100 m und den Streubereich S als einen Durchmesser von D =
10 mm, wobei wir im folgenden als Vereinfachung annehmen, die Trefferwahrscheinlichkeit sei im gesamten Streubereich gleichverteilt (dies trifft
nicht zu, ist aber für unsere grundsätzlichen Überlegungen absolut belanglos).
Das alles soll sich auf eine Versuchsreihe mit dem fest installierten Gewehr beziehen. Da wir die unter irdischen Bedingungen immer vorhandenen
Fehlerquellen ausschalten wollten, verlagerten wir den Versuch „hinreichend weit entfernt“ von störenden Einflüssen in den Weltraum. Für die
verschiedenen Versuche haben wir unsere Raumschiffbesatzung schon mehrfach bemüht (irgendwelchen halbwegs sinnvollen Zwecken muss ihre
Reise ja dienen). Jetzt haben wir keine Probleme mehr mit der Erdanziehung. Und auch die Luft mit ihrem nicht leicht zu berücksichtigenden Einfluss
erschwert unsere Versuche nicht mehr in unkontrollierbarer Weise. Die Zielscheibe sei auf einer Sonde befestigt, die wir vom Raumschiff aus „in den
Raum“ aussenden. Dank der uns zur Verfügung stehenden Präzisionstechnik bereitet uns die exakte Positionierung der Sonde in einem genau definierten Abstand überhaupt keine Mühe.
Da wir uns bereits nicht nur weit von der Erde entfernten, sondern recht weit bereits vom eigentlichen Thema dieses Textes, sei unsere
Aufgabenstellung wiederholt: Es soll untersucht werden, in welchem Maße reproduzierbare Anfangsbedingungen zu reproduzierbaren Ergebnissen
führen. Determiniert der Anfangszustand eines System immer eindeutig den Zustand zu beliebigen Zeiten? Und wie wirken sich die - prinzipiell und
allzeit unvermeidlichen - Fehler in diesen Anfangsbedingungen auf das Ergebnis aus? Also: da hatten wir auf eine Entfernung von einhundert Metern
einen Streudurchmesser von einem Zentimeter. Das macht einen auf diese Entfernung bezogenen relativen Fehler von
Fr = 0,01m/100m = 0,0001 = 10-4.
Wir behaupteten schon, dies sei ein recht optimales Ergebnis. Da wir aber im freien Raum und mit spezieller Technik (wahrhaft) bewaffnet uns
befinden, gehen wir davon aus, diesen Fehler mindesten um den Faktor 100 zu verbessern. Der relative Fehler möge jetzt 10-6 betragen. Das heißt,
bei einer Schussweite von hundert Metern darf die Abweichung maximal 0,1 Millimeter betragen. Ob dies technisch realistisch sein könnte,
interessiert uns nicht. Bezogen auf die Länge des Laufes, welche großzügig mit einem Meter angesetzt wird, würde dies eine Präzision der
Reproduzierbarkeit des Abschusswinkels von 0,001 Millimeter erfordern. Alles kein Problem. Erst einmal nicht.
Jetzt starten wir die Versuchsreihe und werten die Ergebnisse aus. Da das Projektil selbst wesentlich größer ist - angenommen es habe einen
Durchmesser von 10 Millimeter - als der Fehlerkreis stellen wir lediglich fest, dass die Scheibe ein Durchschussloch aufweist, welches einen nur
unwesentlich größeren Durchmesser besitzt als die Geschosse selbst. Jeder Revolverheld Hollywoodscher Provenienz würde erblassen vor Neid.
Das Problem: was sind hundert Meter im All?!
Das macht doch gar nichts. Wir vergrößern die Entfernung. Sie möge jetzt 100 Kilometer netragen. Der relative Fehler ist der gleiche geblieben. Der
absolute Fehler jedoch hat sich um den Faktor 1.000 vergrößert! Der Streukreis beträgt jetzt immerhin 10 Millimeter und kommt damit in die
Größenordnung des Geschossdurchmessers. Das Schussbild sieht plötzlich anders aus. Es ist ein Loch mit 20 Millimeter Durchmesser und nicht ganz sauber Kante.
Das Problem: was sind hundert Kilometer im All?!
Das macht fast gar nichts. Wir vergrößern die Entfernung. Sie möge jetzt 100.000 Kilometer betragen. Der relative Fehler ist der gleiche geblieben.
Der absolute Fehler jedoch hat sich abermals um den Faktor 1.000 vergrößert! Der Streukreis beträgt immerhin 10 Meter und ist damit um zwei
Größenordnungen größer als der des Projektils. Die Flugzeit beträgt beachtliche 200.000 Sekunden. Das sind etwa 56 Stunden. Der
Scheibendurchmesser betrug - wir erinnern uns - ein Meter. Somit ist die Fläche des Streukreises hundert mal größer als die der Scheibe. Wir
müssten schon großes Glück haben, um bei hundert Schüssen überhaupt einen Treffer registrieren zu können.
Das macht fast überhaupt nichts. Wir setzen die Versuchsreihe fort und feuern - sagen wir - 10.000 Schüsse ab. Wenn wir jetzt die Treffer auf der
Scheibe zählen, werden wir etwa hundert Einschüsse ermitteln.
Was das Ganze soll? Gibt es denn nichts banaleres als die hier aufgezählten Fakten? - Das alles ist genaugenommen äußerst banal und an Trivialität
kaum zu überbieten. Auf folgende Aussage kommt es an: Wie klein man den „Anfangsfehler“ auch gestalten mag, er ist als „relativer Fehler“ zuerst
vernachlässigbar, dann aber, lässt man ihm nur genügend Zeit zum Wachsen, wird er irgendwann groß genug sein, um entscheidend in Erscheinung
zu treten. Beziehen wir jetzt „Reproduzierbarkeit“ auf die Möglichkeit des konstanten relativen Fehlers, und damit des linear anwachsenden
absoluten Fehlers, so sind klassisch mechanische System (unsere Schießversuche sind solche klassisch mechanischen Versuche einfachster Art)
eindeutig - und mit abschätzbarem Fehler - reproduzierbar und damit auch determiniert, verstehen wir unter Determiniertheit (s. o.) die Tatsache der
eindeutigen Bestimmtheit des Zustandes eines Systems durch seinen Anfangszustand. Die Zeit spielte hier nicht einmal explizit eine Rolle, da die
Versuchsergebnisse unabhängig waren von der gewählten Geschwindigkeit des Geschosses. (Diese Vereinfachung werden wir noch aufgeben.)
Bei Henri Poincaré konnten wir bereits nachlesen:
|
 Eine sehr kleine Ursache, die wir nicht bemerken, bewirkt einen
beachtlichen Effekt, den wir nicht übersehen können, und dann sagen wir, der Effekt sei zufällig. Wenn die Naturgesetze und der Zustand
des Universums zum Anfangszeitpunkt exakt bekannt wären, könnten wir den Zustand dieses Universums zu einem späteren Moment exakt
bestimmen. Aber selbst wenn es kein Geheimnis in den Naturgesetzen mehr gäbe, so könnten wir die Anfangsbedingungen doch nur
annähernd bestimmen. Wenn uns dies ermöglichen würde, die spätere Situation in der
gleichen Näherung vorherzusagen - dies ist alles, was wir verlangen -, so würden wir
sagen, dass das Phänomen vorhergesagt worden ist und dass es Gesetzmäßigkeiten
folgt. Aber es ist nicht immer so; es kann vorkommen, dass kleine Abweichungen in den
Anfangsbedingungen schließlich große Unterschiede in den Phänomenen erzeugen. Ein
kleiner Fehler zu Anfang wird später einen großen Fehler zur Folge haben. Vorhersagen werden unmöglich, und wir haben ein zufälliges Ereignis. [Hervorhebung W.N.]
|
|
|
Wir also sprachen von dem anwachsenden absoluten Fehler. Unklar in diesem Zusammenhang aber war noch, was „genügend Zeit“ bedeutet und
was wir mit „entscheidend in Erscheinung treten“ meinen. Befassen wir uns als erstes mit dem zweiten Problem und gehen wir es auf verschiedene Art und Weise an.
Jetzt modifizieren wir den letzten Versuch. Wir ersetzen die Zielscheibe durch eine Mechanik, welche ihrerseits der Auslöser für eine zweite
Schussvorrichtung bildet. Dieser Auslöser möge einen Durchmesser von einem Millimeter haben. Bei dem letzten Versuch mit einer
Schussentfernung von 100.000 Kilometern erhielten wir einen Streukreis von 10 Metern. Um aber den Auslöser zu treffen, muss das Projektil einen
gedachten Kreis treffen, der nicht größer sein darf als der Durchmesser dieses Auslöser plus dem doppelten Durchmesser (betrachten wir nur den
Mittelpunkt des Geschosses, so gilt: „...plus dem Durchmesser des Geschosses selbst...“) des Geschosses selbst (wir wollen auch einen Streifschuss
gelten lassen). Das sind im Hinblick auf unsere angenommenen Werte rund 2 Zentimeter. Der Streukreisdurchmesser ist damit 500 mal größer als
der des Zielkreises. Also verhalten sich die Größen beider Flächen wie 1:250.000. Dies auch ist die Wahrscheinlichkeit, den genannten Auslöser zu
treffen. Wir führen jetzt eine Million Versuche durch. Und wenn wir Glück haben, erzielen wir vier Treffer. Oder auch nur drei oder gar sieben. Die
Anzahl der Versuche ist zu gering für sinnvolle Aussagen über die zu erwartende Trefferhäufigkeit. Das Ergebnis: Die Ursache (das Abfeuern des
Schusses aus dem ersten Gewehr) determiniert nicht eindeutig die Wirkung (das Auslösen eines Schusses in der zweiten Vorrichtung)! Hier also
handelt es sich anscheinend um ein akausales Ereignis. Nach unserer bereits erfolgten Definition eines solchen Ereignisses trifft dies jedoch nicht zu.
Die kausale Ursache für das Auslösen des zweiten Schusses wäre das Auftreffen des ersten Geschosses auf die Auslösevorrichtung. Tritt diese
Ursache ein, dann mit Sicherheit auch die Wirkung (wenn keine Störung vorliegt). Hier genau handelt es sich um den Denkfehler, das Auslösen des
ersten Schusses bereits schon als kausale Ursache anzusehen für ein Ereignis, welches erst viel später eintreten wird - oder auch gar nicht. Um jenen
Denkfehler handelt es sich, der mit der unzulässigen Vermischung von Ereignis und Prozess in Verbindung zu bringen ist.
Fassen wir jedoch das Auslösen des ersten Schusses als kausale Ursache für den zweiten auf, zeigt sich uns ein „indeterministisches“ oder
„akausales“ Verhalten. Anstelle des Auslösers für ein zweites Gewehr könnten wir auch eine Lichtschranke setzen, die einen Schalter betätigt,
welche eine Lampe einschaltet oder auch aus. Diese Lampe wird nur in etwa einem von einer Viertelmillion Fällen ein- bzw. ausgeschaltet werden.
Technische Einzelheiten sind uninteressant.
Analysieren wir diesen Vorgang, so gilt als erste Kausalrelation das Betätigen des Abzuges des ersten Gewehres. Dies ist die kausale Ursache für
einen Prozess, den Prozess der sich mit 500 Meter pro Sekunde sich entfernenden Gewehrkugel. Dieser Prozess nun wiederum kann unter
Umständen ein (kausales) Ereignis auslösen. Ein solches Ereignis wurde weiter oben als die „spontane Änderung des Wechselwirkungsverhaltens
mindestens zweier Systeme“ definiert. Dieser Fall liegt dann vor, trifft das Projektil den Schalter. Ob dies aber wirklich geschieht, das bleibt dem Zufall überlassen.
Als nächstes kaskadieren wir die Versuchsanordnung dahingehend, dass der zweite Schuss einen dritten auslöst. Wie groß ist jetzt die
Wahrscheinlichkeit des tatsächlich fallenden Schusses? - Sie beträgt 1:62.500.000.000 = 1,6·10-11. (Es werden einfach die Wahrscheinlicheiten
beider Ereignisse miteinander multipliziert.) Die „vierte Schussgeneration“ wird nur noch mit einer Wahrscheinlichkeit von 4·10-16 eintreten.
Angenommen, wir erzielen eine Schussfolge von zehn Schuss pro Sekunde, so würden wir - grob gerundet - alle 4·1015 Sekunden einen Treffer zu
erwarten haben. Dies sind ungefähr 130 Millionen Jahre (Auch für galaktische Dimensionen ist das bereits eine nicht zu unterschätzende Zeitspanne)!
Das Eintreffen der nächsten „Kausalgeneration“ wäre derart unwahrscheinlich, dass wir ziemlich bedenkenlos das Wort „unmöglich“ verwenden dürfen. Alle 3·1013 (30 Billionen!) Jahre würde - im Mittel - der fünfte Schuss auch ausgelöst werden. Um jedoch überhaupt darüber etwas
aussagen zu können, bedarf es etwa des Hundertfachen an Versuchen. In 3.000 Billionen Jahren - dies ist mehr als das Millionenfache des
angenommenen Alters (unseres annähernd bekannten Teiles) des Universums, würden wir 100 Treffer erzielen - so ungefähr jedenfalls.
Und genau die letzte Aussage eben stimmt nicht! Diese 3.000 Billionen Jahre sind eine Zeitspanne, die durchaus in kosmischen Dimensionen nicht zu
vernachlässigen sind. (Wir werden noch sehen, dass die Aussage, ein Prozess würde 3.000 Billionen Jahre dauern oder auch „nur“ 30 Billionen oder
nicht einmal länger als 30 Milliarden Jahre, ohnehin völlig sinnlos ist.)
Unsere Versuchsanordnung befindet sich „hinreichend weit entfernt“ von „erheblichen Massen“ und damit außerhalb deren Einflussbereiches. Dies
aber gilt nur für kleine und damit vernachlässigbare Zeitspannen. Für 10 Millionen Jahre vielleicht. Selbst für Bruchteile dieses Zeitraumes (z. B. 10
Millisekunden) sind die „gleichen Anfangsbedingungen“ (der Versuchsanordnung) pure Illusion, da zu eben diesen Anfangsbedingungen auch das
„kosmische (Machsche) Umfeld“ gehört. Und letzteres hat sich geringfügig verändert. Geringfügig, das stimmt wirklich. Was aber „geringfügige
Variation des Anfangszustandes“ bedeutet, haben wir lang und breit erörtert, wenngleich wir dies zunächst lediglich auf die Versuchsanordnung an
sich bezogen. Nur: dieses „an sich“ gibt es nicht, es sei denn, wir bitten wieder den „objektiven Raum“ und die „objektive Zeit“ um Hilfe (irgendwie
hängt eben alles zusammen...).
Wie genau wir auch versuchten, die Anfangsbedingungen zu reproduzieren, spielen (u. a.) Kausalbeziehungen eine entscheidende Rolle, dann wächst
der anfänglich kleine und vernachlässigbare Fehler exponentiell an und macht jede Reproduzierbarkeit und damit Prognostizierbarkeit nach
„ausreichend langer Zeit“ illusorisch. Nun erklärten wir aber, die reproduzierten Anfangsbedingungen hängen nur zum Teil von uns selbst ab. Damit
können wir dem Argument begegnen, dass jene Unmöglichkeit der exakten Reproduzierbarkeit lediglich und ausschließlich unser ganz subjektives
und unser ganz ureigenstes Versagen darstellt. Dem also ist nicht so. Folgende Formulierung wäre der Extrakt aus den bisherigen Überlegungen:
|
Der Verlauf von Prozessen hängt im allgemeinen von Ereignissen ab, deren Eintreffen extrem
unwahrscheinlich sein kann. Ereignisse determinieren Prozesse, aber nicht umgekehrt. Auch determinierte Prozesse führen nicht unbedingt zu
determinierten Ereignissen!
|
|
|
Ereignisse sind grundsätzlich Kausalereignisse. Ein Ereignis ist das Eintreten einer kausalen Beziehung. Eine andere Möglichkeit der - objektiven -
Festlegung werden wir schwerlich finden. Kausal-Ereignisse gibt es deshalb, weil das Wechselwirkungsprinzip gilt. Als Gedächtnisstütze:
|
Alles hängt irgendwie mit Allem zusammen und verändert sich in gegenseitiger Abhängigkeit. Es
gibt kein System, welches nicht mit weiteren Systemen im Zusammenhang steht, aber nicht jedes System steht (gleichzeitig) in Verbindung
zu jedem anderen System.
|
|
|
Wie unexakt unsere bisherigen quantitativen Abschätzungen auch sein mochten, sie beziehen sich auf sehr einfache und damit überschaubare
Verhältnisse. Es kommt aber noch schlimmer. Dabei ist es vollkommen belanglos, wie (un)genau die eben getroffenen quantitativen Aussagen gewesen waren.
Abbildung 3
Das gerade beschriebene Beispiel weist, wenngleich konstruiert und sehr stark vereinfacht, auf die Problematik von Prozess und Ereignis hin. Auch
das folgende Beispiel (Abbildung 3) bezieht sich auf nichts anderes, nur kommt hier überhaupt erst der kinematische Aspekt unmittelbar zur Geltung
. Dies will sagen: im ersten Beispiel mit der feststehenden Zielscheibe spielte unter den angenommenen Bedingungen die Geschwindigkeit des
Geschosses unmittelbar keine große Rolle. Jetzt jedoch sollen zwei von verschiedenen Plattformen abgefeuerte Geschosse sich treffen. Nochmals:
Jedes der Geschosse wird - innerhalb der klassischen Begriffswelt - auf der denkbar einfachsten Bahn sich bewegen. Beide Projektile (oder was
sonst es sein möge) bewegen sich „geradlinig und gleichförmig“ und - streng determiniert. In dieser Form der Trägheitsbewegung treffen wir den mit
Abstand einfachsten Prozess an. Zwei dieser primitivsten überhaupt konstruierbaren Prozesse spielen hier die entscheidende Rolle. Unabhängig
voneinander sind sie auch. Analysieren wir auf Basis der vorher angestellten Überlegungen jedoch, wie wahrscheinlich das Ereignis sein wird,
welches im Zusammentreffen beider Geschosse besteht, so würden wir zu dem Schluss kommen, dass dieses Ergebnis mit Sicherheit nie eintrifft. Die
dazugehörende Fehlerrechnung verkneifen wir uns, da sie wesentlich umfangreicher ausfallen würde als die weiter oben angestellte. Das ganze
Missverständnis im Zusammenhang mit der Determinismus-Problematik besteht in der Vorstellung, dass mit der Determiniertheit von Prozessen auch
sämtliche (Kausal-)Ereignisse determiniert seien. Bedenkt man jedoch, dass Ereignisse wesentlich den Verlauf von Prozessen bestimmen (können),
so sind alle Prozesse, welche „Ereignisse enthalten“, natürlich in gleichem Maße unbestimmt.
Stellen wir uns das alles jetzt vor dem konkreten Hintergrund der konkreten und komplexen materiellen Gegebenheiten vor, so müsste klar werden,
dass der Gedanke von der durchgängigen Determiniertheit allen Weltgeschehens wirklich nur ein Gedanke sein kann. Auch in unseren - geradezu
abschreckend primitiven - Beispielen mit den Schießübungen fällt es schwer, wirklich reproduzierbare Ergebnisse bei reproduzierten
Anfangsbedingungen zu erzielen. Selbst, gelänge uns eine immer größere Präzision, so bleiben die gleichen Anfangsbedingungen pure Illusion.
Letzteres um so mehr, je länger eine Versuchsserie dauert. Mit der letzten Aussage finden wir den Weg zur Problemstrecke der Definition und/oder
der Bestimmung jener Anfangswerte, die, wären sie bekannt, alles Kommende eindeutig festlegen würden. Wir müssen Anfangsorte und
Anfangsgeschwindigkeiten (in bezug worauf?) mit absoluter Genauigkeit bestimmen, geht es um die Prognostizierbarkeit oder festlegen, geht es um
die Reproduzierbarkeit. Beides ist unmöglich. Da aber jeder noch so kleine Fehler irgendwann einmal so groß werden wird, dass nicht mehr
entscheidbar ist, ob ein Ereignis eintritt oder auch nicht, wird spätestens auch dann der Gesamtprozess mit jener Unsicherheit behaftet sein, die nicht
mehr abschätzbar ist.
Je mehr Prozesse von Kausalketten bestimmt werden, desto stärker sind solche Prozesse vom Zufall geprägt. Die Anfangszustände werden nicht auf
ewige Zeiten alles Geschehen eindeutig festlegen. Das können wir auch so formulieren: Je länger Prozesse dauern, desto mehr werden sie mit hoher
Wahrscheinlichkeit von Kausalereignissen beeinflusst, und damit nimmt ihre zukunftbezogene Unbestimmtheit zu.
Andererseits lassen sich aus der Analyse des Zustandes eines gegebenen Prozesses im allgemeinen keine eindeutigen Schlüsse über das
Kausalereignis ziehen, welches jenen Prozess bestimmte oder wenigstens maßgeblich beeinflusste. Hierzu soll ein einfaches Beispiel zur
Erläuterung dienen, wobei uns das bereits aus dem vorigem Kapitel nützliche Pendel abermals als Hilfe dienen soll. Ein solches Pendel, einmal in
Schwingungen versetzt, würde bis in alle Ewigkeit seine Pendelbewegung ausführen, gäbe es nicht die unvermeidlichen Reibungsverluste. Dadurch
vermindert sich nach und nach die Schwingungsweite, bis schließlich das Pendel völlig aufhört zu schwingen. Tatsache ist: Die Pendelschwingung
ist ein ganz und gar mustergültig determinierter Prozess, der sich, wie es sich für einen solchen geziemt, in Vergangenheit und Zukunft verfolgen
lässt. Die Zukunft liegt offen vor uns. Sind die Parameter des Systems Pendel bekannt, so lässt sich auch berechnen, wie der Verlauf der
gedämpften Schwingung sich vollzieht. Angenommen, wir stellen ein solches Pendel auf und verlassen das Zimmer. Dann kommen wir zurück und
stellen fest, dass erstens sich eine zweite Person im Raum befindet, und wir entdecken zweitens, dass das vorher in Ruhe befindliche Pendel
Schwingungen vollführt. Wir bestimmen - wie auch immer - die Parameter der Pendelvorrichtung (aktuelle Amplitude und die Abnahme der
Amplitude in Abhängigkeit von der Zeit), dann sind wir in der Lage vorauszusagen, wann die Schwingungsamplitude sich aufgrund der
unvermeidlichen Reibungsverluste so weit verringert haben wird, dass wir die Schwingungen nicht mehr wahrnehmen können. Ebensogut scheint
es möglich, zurückzuverfolgen, wie sich das System in der Vergangenheit verhalten haben musste. Doch genau das ist nicht der Fall.
Aus der Kenntnis der Informationen, die uns das Pendel selbst - und nur das Pendel - zur Verfügung stellt, ist die Zurückverfolgung in
die Vergangenheit nur bedingt möglich! Es ist nicht durchführbar, den Zeitpunkt zu bestimmen, wann das Pendel in Schwingungen versetzt
wurde und wie groß die Anfangsamplitude war (beide Größen sind voneinander abhängig)! Wir können die zweite im Zimmer befindliche Person
befragen, die, so nehmen wir an, das Pendel angestoßen haben muss. Kann oder will diese Person eine solche Information nicht liefern, werden wir
nie erfahren, was wirklich passiert war.
Das Anstoßen dieses Pendels aber genau ist ein solcher Vorgang, den wir lang und breit als Kausalereignis diskutierten. Verallgemeinern wir die
anhand des einfachen Beispiels gewonnen Erkenntnis, so dürfen wir behaupten: Prozesse, die von Kausalereignissen bestimmt werden, „vergessen“
ihre Vergangenheit! Diese „Vergesslichkeit“ jedoch ist das, war wir mit Nichtumkehrbarkeit oder Irreversibilität in Verbindung bringen wollen!
Umgekehrt formuliert: Irreversible Prozesse sind durch ihre „Vergesslichkeit“ die Vergangenheit betreffend gekennzeichnet, welche ihrerseits im
Zusammenhang steht mit der Kausalität. Dieser letzten Konsequenz entgehen wir durch die Annahme einer „objektiven Zeit“. Diese Zeit versucht
das Wechselwirkungsprinzip zu umschiffen, welches da lautet (für diejenigen, die es immer noch nicht auswendig hersagen können):
|
Alles hängt irgendwie mit Allem zusammen und verändert sich in gegenseitiger
Abhängigkeit. Es gibt kein System, welches nicht mit weiteren Systemen im Zusammenhang steht, aber nicht jedes System steht
(gleichzeitig) in Verbindung zu jedem anderen System.
|
|
|
Beziehen wir jetzt noch die Überlegungen ein, die verbunden sind mit den für die Bewegungen notwendigen Bezugssystemen und die Definition eines
Zeitmaßstabes, so müsste klar werden, dass dann erst recht niemals die „gleichen Anfangsbedingungen“ definierbar sind. Der Zeitbegriff jedenfalls -
das ist bereits bekannt - suggeriert die Illusion, dass scheinbar gleichzeitig alle - aber auch alle! - Prozesse an einem einheitlichen „Zeittakt hängen“.
Wäre dem so, dann gäbe es wirklich keinen objektiven Zufall.
|
Entweder es gibt den objektiven Zufall oder die objektive Zeit.
|
|
|
Bitte beachten, dass „die Zeit“ als praktizierter Begriff auf eine eigenständige Realität - Objekt - hinweist, während „der Zufall“ als Bezeichnung für
die Zufälligkeit - Relation - bestimmter Ereignisse steht. Vgl. Die Aussagen in Der Pygmalion-Effekt.
|
Die Aussage „es existiert der Zufall und die objektive Zeit“ ist ein Widerspruch in sich. In der objektiven Zeit finden wir die konkrete Verkörperung des Laplaceschen Dämons, der nicht wahrhaben will, dass es auch voneinander unabhängige Systeme und damit Prozesse gibt. Jene „objektive Zeit“ setzt den zweiten Teil der Aussage des Wechselwirkungsprinzips logisch außer Kraft: „...aber nicht jedes System steht (gleichzeitig) in Verbindung zu jedem anderen System“.
|
|
|
Lesen wir die eingangs des Kapitels zusammengesponnene Geschichte mit dem Urlauber unter dem Gesichtspunkt der Determiniertheit von
Prozessen und Ereignissen, so müssen wir zu dem Resultat kommen, dass wir uns zunächst mit zwei Prozessen zu beschäftigen haben: es handelt sich
um die Lebensläufe zweier Personen. Jeder dieser Prozesse ist weitgehend „ereignisdeterminiert“. Betrachten wir unser eigenes Leben, so kommen
wir oft zu der Einsicht, dass dieses Leben von vielen, zum Teil beeinflussbaren und zum Teil nicht von uns abhängigen Ereignissen bestimmt wird.
Diese Ereignisse nun wiederum hängen von anderen Ereignissen und damit Prozessen ab, welche ihrerseits... „Wenn ich damals...“ oder „hätte ich
doch...“ oder auch „zum Glück habe ich...“ usw. usf... (Hätte der Hund nicht gesch... Vergleichen wir das „wahre Leben“ mit unseren recht sinnlos
erscheinenden Schießversuchen im freien Raum, so kommen wir nicht umhin, zu akzeptieren, dass es für wirklich starr determinierte Prozesse so gut
wie keinen Spielraum gibt. So erscheint es unwichtig, ob das zweite Geschoss das erste trifft oder auch nicht. Gehen wir aber die Straße entlang und
fällt ein Ziegel vom Dach, der sich lockerte, so ist es durchaus nicht unerheblich, ob das - unvorhersehbare! - Ereignis „Ziegel trifft Kopf” eintritt
oder auch nicht. Für den - wahrhaft - Betroffenen ist dies einigermaßen von Bedeutung. Für denjenigen also, der seinen Kopf hinhalten musste, kann
solch Ereignis sehr unangenehm bis tödlich sein. (Das hängt von der Fallhöhe ab.)
|
Prinzipiell sind alle Prozesse nicht im klassischen Sinne determiniert.
Dies ist die Regel. Und wie es Regeln in der Regel so an sich haben, gibt es in der Regel keine Regel ohne Ausnahme.
Jeder Prozess ist innerhalb des Zeitraumes, in dem mit Sicherheit keine
Kausalereignisse eintreten werden, im allgemeinen stetig (im klassischen Sinne also) determiniert. Für diesen
Zeitraum sind diese Prozesse reversibel, das heißt, sie lassen sich auch in die Vergangenheit zurückverfolgen. Für
jeden Prozess ist eine solche durchschnittliche charakteristische Zeitspanne prinzipiell angebbar.
|
|
|
Auf die genannte „charakteristische Zeitspanne“ kommt es an. Diese ist für verschiedene Prozesse naturgemäß ebenfalls verschieden. Beobachten
wir die kosmischen Objekte (innerhalb unseres Sonnensystems zum Beispiel), so haben wir ein „stetig determiniertes System“ vor uns.
Vergangenheit und Zukunft liegen vor uns ausgebreitet. Dies aber liegt an der - an unseren Vorstellungen gemessenen - extrem langen Zeiträumen
der „stetigen Determiniertheit“. Die kosmischen Prozesse laufen eben besonders langsam ab.
Die “stetige Determiniertheit” des Sonnensystems gilt für die Vergangenheit nicht uneingeschränkt. Anhand der (mechanischen) Parameter des
Systems lässt sich nicht dessen Alter bestimmen. Wir wissen, dass es irgendwann entstanden sein muss (Größenordnung vier bis fünf Milliarden
Jahre), aber dieses Ergebnis lässt sich nicht durch “Zurückrechnung” des Bewegungsablaufes der Planeten ermitteln. Hierzu müssen andere
Informationen sachgerecht interpretiert werden.
Aus der Frage: „Warum verhalten sich die Quantenobjekte (zum Beispiel) nicht starr determiniert?“ wird die Frage: „Wie kommt es
bloß, dass sich das Planetensystem (zum Beispiel) fast beliebig in Vergangenheit und Zukunft verfolgen lässt?“. Das erste ist die Regel;
das zweite die Ausnahme! Die Ausnahme jedoch wurde zum Maßstab des wissenschaftlichen Denkens!
Die uns bekannte Form der Determiniertheit des Sonnensystems ist so selbstverständlich nicht, wie es auf dem ersten Blick erscheinen mag. Im
Allgemeinen verhalten sich Mehr-Massen-Systeme mit abstandsabhängigen Zentralkräften chaotisch und instabil. Ein notwendiges, aber noch nicht
hinreichendes, Stabilitätskriterium besteht darin, dass eine “große Zentralmasse” stabilisierend wirkt. Nähere Informationen sind im Text Chaos zu finden.
Eine Sekunde ist eine Zeiteinheit, die wir sehr gut erfassen. Eine zehntel Sekunde stellt auch nichts Exotisches dar. Die hundertstel Sekunde
entscheidet mitunter über Sieg und Niederlage im Sport. Auch eine tausendstel Sekunde bildet selbst für relativ einfache mechanische Systeme keine
nennenswerte Grenze. Für die Verschlüsse normaler Fotoapparate ist dies noch nicht einmal eine extreme Leistung. Der Hochfrequenztechniker
begibt sich in die Gefilde der Mikrosekunden oder gar Nanosekunden. Diese Zeiteinheiten sind dann nur noch abstrakt erfassbar, anschaulich
überhaupt nicht mehr.
Das Alter unseres Sonnensystems beziffert sich auf ca. 5 Milliarden Jahre; dies sind so etwa 1,5·1016 Sekunden. Eine Nanosekunde beträgt, in
Zehnerpotenzen dargestellt, 10-9 Sekunden. Doch ist jene Zeitspanne im Bereich der atomaren Dimensionen „eine Ewigkeit“. Wollten wir für die
Prozesse innerhalb eines Atomkerns eine entsprechende „Zeitspanne der stetigen Determiniertheit“ angeben, so kommen wir bequem auf Zeiten
vielleicht, die unterhalb von 10-20 Sekunden anzusiedeln wären. Wir selbst werden vielleicht 2·109 Sekunden alt. Das Alter des Weltalls wird auf
etwa 3·1017 Sekunden geschätzt, welches damit „nur“ 108 mal so alt ist wie wir selbst es werden können. Setzen wir die Nanosekunde (= 10-9
Sekunden, eine für uns prinzipiell nicht anschaulich zugängliche Zeitspanne) in Relation zu den gerade erwähnten 10-20 Sekunden, so erhalten wir ein
Verhältnis von 1:1011.
Was das Ganze soll? - Vielleicht der Versuch der Veranschaulichung völlig unanschaulicher Beziehungen und der Versuch, sich vor Augen zu halten,
warum die Mikroobjekte sich dermaßen unsinnig verhalten. Diese Quantenobjekte verhalten sich nicht deshalb so maßlos unverständlich, weil sie es
nun einmal so an sich haben, weil „die Gesetze der Quantenmechanik“ es so und nicht anders erfordern, sondern weil der Mikrokosmos sich zeitlich
dermaßen außerhalb der uns zugänglichen Welt befindet, wie es „außerhalber“ fast nicht mehr geht! (Wir erwähnten an anderer Stelle 40
Größenordnungen, die Gravitation und Kernkraft voneinander trennen.)
Hierzu gäbe es noch viele Seiten zu beleuchten. Wir lassen es an dieser Stelle sein, weil es im Rahmen unserer Überlegungen zu weit führen würde.
Worauf es also ankommt, ist festzustellen: Stetig determinierte Prozesse bilden prinzipiell die Ausnahme. dass aus unserer ganz speziellen Sicht auf
unserer Ebene der Materiestrukturen bestimmte Prozesse stetig determiniert sind, liegt einzig und allein an den ganz speziellen konkreten
Verhältnissen unseres kosmischen Umfeldes und unseres „persönlichen Zeitmaßstabes“. Diese „ganz speziellen Verhältnisse“ aber waren - und sind -
weitgehend bestimmend für das, was wir „physikalisches Weltbild“ nennen. Diese „ganz speziellen Verhältnisse“ sind verantwortlich dafür, was wir
in diesem Text „mechanistisches“ oder „statisches Paradigma“ nannten. Dass natürlich diese Auffassung zu Problemen führte als man begann, die
„Bausteine der Materie“ zu untersuchen, wurde nicht zum Anlass genommen, über jene „statischen Anfangsvorstellungen“ nachzudenken, sondern
das mechanistische Weltbild wurde in Frage gestellt, ohne aber wirklich zu wissen, was dieses nun wirklich auszeichnete. Nicht die Mechanik hat
versagt, sondern die Statik! Das statische Denken musste früher oder später sich als inadäquat herausstellen. Dieses „früher oder später“ hatten wir
bereits konkret genannt. Es war die Wende vom 19. zu 20. Jahrhundert. Aber das alles kennen wir schon.
Fassen wir das bisher gesagte zusammen:
- Die wichtigsten Begriffe im gerade behandelten Zusammenhang waren: System, Prozess, Zustand, (Kausal-)Ereignis.
- Sind voneinander unabhängige Prozesse korreliert, d. h. lassen sich die Zustände eines Systems den Zuständen eines zweiten Systems
zuordnen, obwohl diese Systeme nicht unmittelbar in Verbindung stehen, so gelten diese Prozesse als determiniert.
- Unter ganz bestimmten und ganz speziellen Bedingungen darf die in (2.) genannte Korrelation durch die Korrelation mit einem unabhängigen
Parameter ersetzt werden, der die Rolle der „unabhängigen Variablen“ übernimmt und welchen wir „Zeit“ nennen. Dann determiniert der
Zustand eines Systems zum gegebenen Zeitpunkt den Zustand des Systems zu beliebigen Zeiten.
- Ein Ereignis ist das Eintreten einer Kausalrelation, wenn also zwei Systeme miteinander in Kontakt treten, die vor diesem Ereignis unabhängig
voneinander waren.
- Ereignisse wären dann - und nur dann - determiniert, wenn wir die unter (3.) aufgeführte Zeit wirklich als eine unabhängige Realität
akzeptieren. Ansonsten müssen Ereignisse - auch determinierter Prozesse - nicht unbedingt ebenfalls determiniert sein. (Gemeint ist hier
eindeutig die objektive Determiniertheit, unabhängig davon ob Prozesse „erzeugt“ oder beobachtet werden.)
- Wenngleich Ereignisse selbst nicht determiniert sind (bzw. „nur“ statistisch), so werden andererseits Prozesse wesentlich durch Ereignisse
bestimmt.
- Die Schwierigkeit der Kausalitäts- und Determinismusproblematik liegt in der statischen Denkweise begründet. (Ich wiederholte sie oft genug.
)
Wir haben in diesem Kapitel - vielleicht - einige Fragen beantwortet. Folgende Probleme aber bleiben offen:
- Wie bringen wir in das von uns herbeigeredete Chaos wieder Ordnung? Denn soviel ist klar: der Zufall ist die eine Seite der Medaille. Wie
sieht die andere aus?
- Wir betrachteten das Wechselwirkungsprinzip aus zwei Blickwinkeln, konnten aber bisher theoretisch nicht begründen, warum die Aussage „.
..aber nicht jedes System steht (gleichzeitig) in Verbindung zu jedem anderen System“ wirklich der Wahrheit entspricht.
- Welche Konsequenzen ergeben sich in Hinblick auf „kosmologische Weltmodelle“? Wie wäre die Urknallhypothese hier einzuordnen. Dies ist
eine sehr spezielle Frage. Und obwohl wir nicht vorhaben, spezielle Fragen zu beantworten (hierzu wäre nicht nur Phantasie vonnöten,
sondern auch das unentbehrliche mathematische Rüstzeug), so gibt es dennoch Konsequenzen prinzipieller Natur, die durchaus
untersuchungswürdig und untersuchungsfähig sind.
- Weiter oben schnitten wir die Probleme an, die im Zusammenhang stehen mit der Vorhersagbarkeit von Prozessen. Dieses Thema ist auf das
engste verknüpft mit der Realisierung von Messprozessen und der Möglichkeit der Arbeit mit mathematischen Modellen in Form von
Differentialgleichungssystemen oder bestimmten Formen der Computersimulation.
Wurde von Kausalereignis gesprochen, so war dies mit der „spontanen Änderung des Wechselwirkungsverhalten mindestens zweier Systeme“
verbunden. Dabei wurde zwischen Prozess und Ereignis unterschieden. Diese Darstellung lässt die Frage offen, was im Allgemeinen darunter zu
verstehen sei. Die quantitative Abgrenzung fehlt. Auch Ereignisse sind Prozesse - auf einer anderen Zeitskala gewissermaßen. Wir müssen bedenken,
dass die in diesem Kapitel definierte Kausalbeziehung als der in der Realität oft vorzufindende Grenzfall betrachtet werden muss:
|
Eine Kausalrelation mindestens zweier Systeme liegt vor, wenn eine
spontane Veränderung des Wechselwirkungsverhaltens dieser Systeme nachweisbar ist, die darin besteht, dass
Wechselwirkungen zwischen diesen Systemen auftreten, die vor der Kausalbeziehung nicht bzw. in qualitativ oder
quantitativ anderer Form bestanden.
|
|
|
Die Formulierung „in quantitativ anderer Form“ lässt auch Wechselwirkungen zu, die zu einem gegebenen Zeitpunkt zwar vorhanden sind, aber zu
eben diesem Zeitpunkt das Geschehen nur unwesentlich beeinflussen, indem sie unterhalb des „Rauschpegels“ liegen. Nur ist dieses „unwesentlich“
kein endgültiges Prädikat. Was zu einem gegebenen Zeitpunkt noch unwesentlich ist, kann zu einer späteren Zeit schon sehr maßgeblich in
Erscheinung treten. Und auch jene Formen von Wechselwirkungen müssen wir dabei mit erfassen, die als hochgradig nichtlineare Beziehungen sich
darstellen. Die „spontane Änderung des Wechselwirkungsverhaltens“ erweist sich hier als die extremste Form der Nichtlinearität.
[Home] [Seitenanfang]
|
